0% found this document useful (0 votes)
145 views7 pagesFinite Difference Approximation: Using Taylor Series Expansion
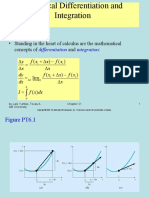
Finite difference approximations can be derived using Taylor series expansions. This document describes finite difference approximations for the first and second derivatives. The first derivative can be approximated using forward, backward, or central differencing, with central differencing being second-order accurate. The second derivative is approximated using forward, backward, or central differencing, with all three approximations being first-order accurate. Equations for each approximation are presented.
Uploaded by
Mine RHCopyright
© Attribution Non-Commercial (BY-NC)
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
145 views7 pagesFinite Difference Approximation: Using Taylor Series Expansion
Finite difference approximations can be derived using Taylor series expansions. This document describes finite difference approximations for the first and second derivatives. The first derivative can be approximated using forward, backward, or central differencing, with central differencing being second-order accurate. The second derivative is approximated using forward, backward, or central differencing, with all three approximations being first-order accurate. Equations for each approximation are presented.
Uploaded by
Mine RHCopyright
© Attribution Non-Commercial (BY-NC)
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 7