1.
(a)
valid approach
(M1)
e.g. b 2 4ac, 0, 4k 2 42k 1
correct equation
A1
e.g. (4k)2 4(2k)(1) = 0, 16k2 = 8k, 2k2 k = 0
correct manipulation
e.g. 8k 2k 1,
(b)
A1
8 64
32
1
2
A2
recognizing vertex is on the x-axis
N3
N1
M1
e.g. (1, 0), sketch of parabola opening upward from the x-axis
P0
A1
[7]
2.
(a)
f (x) = 10(x + 4)(x 6)
(b)
METHOD 1
attempting to find the x-coordinate of maximum point
A1A1
N2
N4
N4
N0
(M1)
e.g. averaging the x-intercepts, sketch, y = 0, axis of symmetry
attempting to find the y-coordinate of maximum point
(M1)
e.g. k = 10(1+ 4)(1 6)
f (x) = 10(x 1)2 + 250
A1A1
METHOD 2
attempt to expand f (x)
(M1)
e.g. 10(x2 2x 24)
attempt to complete the square
(M1)
e.g. 10((x 1)2 1 24)
f (x) = 10(x 1)2 + 250
(c)
attempt to simplify
A1A1
(M1)
e.g. distributive property, 10(x 1)(x 1) + 250
correct simplification
A1
e.g. 10(x2 6x + 4x 24), 10(x2 2x +1) + 250
f (x) = 240 + 20x 10x2
(d)
(i)
valid approach
IB Questionbank Maths SL
AG
(M1)
�e.g. vertex of parabola, v(t) = 0
t =1
(ii)
A1
recognizing a(t) = v(t)
a(t) = 20 20t
speed is zero t = 6
a(6) = 100 (m s2)
N2
(M1)
A1A1
(A1)
A1
N3
7
[15]
3.
(a)
evidence of setting function to zero
e.g. f(x) = 0, 8x = 2x2
evidence of correct working
e.g. 0 = 2x(4 x),
A1
8 64
4
x-intercepts are at 4 and 0 (accept (4, 0) and (0, 0), or x = 4, x = 0)
(b)
(M1)
(i)
x = 2 (must be equation)
(ii)
substituting x = 2 into f(x)
y=8
A1A1 N1N1
A1
N1
(M1)
A1
N2
[7]
4.
(a)
q = 2, r = 4 or q = 4, r = 2
(b)
x = 1 (must be an equation)
(c)
substituting (0, 4) into the equation
e.g. 4 = p(0 (2))(0 4), 4 = p(4)(2)
(M1)
correct working towards solution
e.g. 4 = 8p
4 1
p =
8 2
(A1)
A1A1
N2
A1
N1
A1
N2
[6]
IB Questionbank Maths SL
�5.
(a)
(b)
f (x) = 3(x2 + 2x + 1) 12
= 3x2 + 6x + 3 12
= 3x2 + 6x 9
A1
A1
AG
N0
(i)
vertex is (1, 12)
A1A1
N2
(ii)
x = 1 (must be an equation)
A1
N1
(iii)
(0, 9)
A1
N1
(iv)
evidence of solving f (x) = 0
e.g. factorizing, formula,
correct working
e.g. 3(x + 3)(x 1) = 0, x
(M1)
A1
6 36 108
6
(3, 0), (1, 0)
A1A1 N1N1
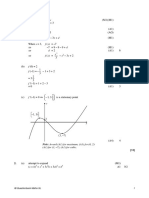
(c)
y
x
3
9
12
A1A1
N2
A1A1A1
N3
Notes: Award A1 for a parabola opening upward,
A1 for vertex and intercepts in
approximately correct positions.
(d)
p 1
, t = 3
q 12
(accept p = 1, q = 12, t = 3)
[15]
IB Questionbank Maths SL
�6.
(a)
evidence of attempting to solve f (x) = 0
evidence of correct working
e.g. x 1x 2,
1 9
2
intercepts are (1, 0) and (2, 0) (accept x = 1, x = 2)
(b)
evidence of appropriate method
e.g. xv
(M1)
A1
A1A1 N1N1
(M1)
x1 x2
b
, xv
, reference to symmetry
2
2a
xv = 0.5
A1
N2
[6]
7.
(a)
(b)
For a reasonable attempt to complete the square, (or expanding)
e.g. 3x2 12x + 11 = 3(x2 4x + 4) + 11 12
f(x) = 3(x 2)2 1 (accept h = 2, k = 1)
(M1)
A1A1
N3
METHOD 1
Vertex shifted to (2 + 3, 1 + 5) = (5, 4)
so the new function is 3(x 5)2 + 4 (accept p = 5, q = 4)
M1
A1A1
N2
METHOD 2
g(x) = 3((x 3) h)2 + k + 5 = 3((x 3) 2)2 1 + 5
= 3(x 5)2 + 4 (accept p = 5, q = 4)
M1
A1A1
N2
[6]
8.
2 1 2 1 2 1 1 0 0 0
6
k
3 4 3 4 3 4 0 1 0 0
6
7
M2 =
18 19
12 6
6M =
18 24
5 0 k 0 0 0
0 5 0 k 0 0
k=5
(A1)
A2
A1
A1
A1
N2
[6]
IB Questionbank Maths SL
�9.
(a) Evidence of completing the square
f(x) = 2(x2 6x + 9) + 5 18
= 2(x 3)2 13 (accept h = 3, k = 13)
(b)
Vertex is (3, 13)
(c)
x = 3 (must be an equation)
(d)
evidence of using fact that x = 0 at y-intercept
y-intercept is (0, 5) (accept 5)
(e)
METHOD 1
evidence of using y = 0 at x-intercept
e.g. 2(x 3)2 13 = 0
evidence of solving this equation
13
e.g. (x 3)2 =
2
13
(x 3) =
2
13
26
3
x=3
2
2
6 26
x=
2
p = 6, q = 26, r = 2
METHOD 2
evidence of using y = 0 at x-intercept
e.g. 2x2 12x + 5 = 0
evidence of using the quadratic formula
12 12 4 2 5
2 2
6 26
12 104
x=
4
2
(M1)
(A1)
A1
N3
A1A1
N2
A1
N1
(M1)
A1
N2
(M1)
(M1)
A1
A1
A1A1A1
N4
(M1)
(M1)
x=
p = 12, q = 104, r = 4 (or p = 6, q = 26, r = 2)
A1
A1
A1A1A1
N4
[15]
IB Questionbank Maths SL
�10.
(a)
METHOD 1
Using the discriminant = 0 (q2 4(4)(25) = 0)
M1
q = 400
q = 20, q = 20
A1A1
N2
METHOD 2
Using factorizing:
(2x 5)(2x 5) and/or (2x + 5) (2x + 5)
q = 20, q = 20
M1
A1A1
N2
(b)
x = 2.5
A1
N1
(c)
(0, 25)
A1A1
N2
[6]
11.
(a)
(b)
(i)
m=3
A2
N2
(ii)
p=2
A2
N2
Appropriate substitution
M1
eg 0 = d(1 3)2 + 2, 0 = d(5 3)2 + 2, 2 = d(3 1)(3 5)
1
2
A1
N1
[6]
12.
(a)
p = 1 and q = 3 (or p =3, q = 1)
(accept (x + 1)(x 3))
IB Questionbank Maths SL
(A1)(A1) (C2)
�(b)
EITHER
by symmetry
(M1)
OR
differentiating
dy
= 2x 2 = 0
dx
(M1)
OR
Completing the square
(M1)
x2 + 2x 3 = x2 2x + 1 4 = (x 1)2 4
THEN
x = 1, y = 4
(c)
(so C is (1, 4))
(A1)(A1)(C2)(C1)
(A1) (C1)
(accept (0, 3))
[6]
13.
Discriminant = b2 4ac (= (2k)2 4)
>0
Note: Award (M1)(M0) for 0.
(A1)
(M2)
(2k)2 4 > 0 4k2 4 > 0
EITHER
4k2 > 4 (k2 > 1)
(A1)
OR
4(k 1)(k + 1) > 0
(A1)
OR
(2k 2)(2k + 2) > 0
(A1)
THEN
k < 1 or k > 1
(A1)(A1) (C6)
Note: Award (A1) for 1 < k <1.
[6]
14.
(a)
h3
(A1)
k 2
(A1)
IB Questionbank Maths SL
�(b)
(c)
(d)
f ( x) ( x 3)2 2
x2 6 x 9 2 (must be a correct expression)
(A1)
x2 6 x 7
(AG)
(A2)
f ( x) 2 x 6
(i)
tangent gradient 2
gradient of L
1
2
(A1)
(ii)
(A1)
(N2)
EITHER
equation of L is y
1
xc
2
c 1 .
(M1)
(A1)
1
x 1
2
OR
1
y 1 ( x 4)
2
(A2)
(iii)
(N2)
EITHER
x2 6 x 7
1
x 1
2
2 x2 11x 12 0
(M1)
(may be implied)
(A1)
(2 x 3)( x 4) 0 (may be implied)
(A1)
x 1.5
(A1)
(N3)
OR
x2 6 x 7
x 1.5
(A3)
1
x 1 (or a sketch)
2
(M1)
(N3)
8
[13]
IB Questionbank Maths SL
�15.
One solution discriminant = 0
(M2)
32 4k = 0
(A2)
9 = 4k
9
1
k = 2 , 2.25
(A2) (C6)
4
4
Note: If candidates correctly solve an incorrect equation,
award M2 A0 A2(ft), if they have the first line or equivalent,
otherwise award no marks.
[6]
16.
(a)
a = 3, b = 4
f (x) = (x 3)2 + 4
(b)
y = (x 3)2 + 4
(A1)
A1 (C2)
METHOD 1
x = (y 3)2 + 4
x 4 = (y 3)2
x4 =y3
(M1)
x4 +3
(A1)
y=
(M1)
3
METHOD 2
y 4 = (x 3)2
y4 =x3
(M1)
(M1)
y4 +3=x
x4 +3
y=
1
f (x) =
(c)
x4 +3
x4
(A1)
(A1)(C1)
[6]
17.
(a)
(b)
(i)
h=1
(A2) (C2)
(ii)
k=2
(A1) (C1)
a(l + l)2 + 2 = 0
a = 0.5
(M1)(A1)
(A1) (C3)
[6]
18.
(a)
2x2 8x + 5 = 2(x2 4x + 4) + 5 8
= 2(x 2)2 3
=> a = 2, p = 2, q = 3
IB Questionbank Maths SL
(M1)
(A1)(A1)(A1)
(C4)
9
�(b)
Minimum value of 2(x 2)2 = 0 (or minimum value occurs when x = 2) (Ml)
Minimum value of f (x) = 3
(A1) (C2)
OR
Minimum value occurs at (2, 3)
(M1)(A1) (C2)
[6]
19.
y = (x +2)(x 3)
= x2 x 6
Therefore, 0 = 4 2p + q
(M1)
(A1)
(A1)(A1)(C2)(C2)
OR
y = x2 x 6
(C3)
OR
0 = 4 2p + q
0 = 9 + 3p + q
p = 1, q = 6
(A1)
(A1)
(A1)(A1)(C2)(C2)
[4]
20.
8
y = x2
y = 53(x4)
4
2
2
q=5
k = 3, p = 4
(A1) (C1)
(A3) (C3)
[4]
IB Questionbank Maths SL
10
�21.
4x2 + 4kx + 9 = 0
Only one solution b2 4ac = 0
16k2 4(4)(9) = 0
k2 = 9
k = 3
But given k > 0, k = 3
(M1)
(A1)
(A1)
(A1) (C4)
OR
One solution (4x2 + 4kx + 9) is a perfect square
4x2 + 4kx + 9 = (2x 3)2 by inspection
given k > 0, k = 3
(M1)
(A2)
(A1) (C4)
[4]
22.
Graph of quadratic function.
Expression
(A1) (C1)
(A1) (C1)
b2 4ac
(A1) (C1)
(A1) (C1)
[4]
23.
(a)
x2 3x 10 = (x 5)(x + 2)
(b)
x2 3x 10 = 0 (x 5)(x + 2) = 0
x = 5 or x = 2
(M1)(A1) (C2)
(M1)
(A1) (C2)
[4]
24.
1
,q=2
2
or vice versa
(a)
p=
(b)
By symmetry C is midway between p, q
Note: This (M1) may be gained by implication.
x-coordinate is
(A1)(A1) (C2)
1 2 3
2
2
4
(M1)
(A1) (C2)
[4]
IB Questionbank Maths SL
11
�25.
(7 x)(1 + x) = 0
x = 7 or x = 1
7 1
B: x =
= 3;
2
y = (7 3)(l + 3) = 16
(M1)
(A1)(C1)(C1)
(A1)
(A1) (C2)
[4]
IB Questionbank Maths SL
12