0% found this document useful (0 votes)
273 views33 pagesStanding Waves, Beats, and Group Velocity
1. Standing waves occur when two waves of the same frequency travel in opposite directions, resulting in a stationary wave pattern of nodes and antinodes.
2. Beats occur when two waves of nearly the same but different frequencies interfere, producing a modulated waveform with a frequency equal to the difference between the two frequencies.
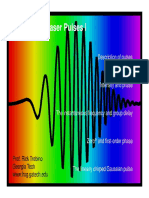
3. Group velocity refers to the velocity at which the envelope or pulse of a wave packet propagates, and is defined as the derivative of the frequency with respect to the wavenumber. It describes how information or energy is transmitted through a medium by a group of waves.
Uploaded by
Siddharth RajamohananCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
273 views33 pagesStanding Waves, Beats, and Group Velocity
1. Standing waves occur when two waves of the same frequency travel in opposite directions, resulting in a stationary wave pattern of nodes and antinodes.
2. Beats occur when two waves of nearly the same but different frequencies interfere, producing a modulated waveform with a frequency equal to the difference between the two frequencies.
3. Group velocity refers to the velocity at which the envelope or pulse of a wave packet propagates, and is defined as the derivative of the frequency with respect to the wavenumber. It describes how information or energy is transmitted through a medium by a group of waves.
Uploaded by
Siddharth RajamohananCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 33