0% found this document useful (0 votes)
139 views42 pagesPipe Flow Pressure Dynamics
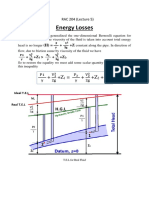
Pressure drop occurs as fluid flows through pipes due to friction between the fluid and pipe wall. This pressure drop must be overcome by pumps to maintain fluid flow. Pressure drop is caused by factors like friction and viscosity, and can be calculated using equations that consider pipe diameter, fluid properties, and flow characteristics like laminar or turbulent flow. Minor losses also contribute to pressure drop and can be estimated using resistance coefficients for components like sudden enlargements.
Uploaded by
Nixon RamsaranCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
139 views42 pagesPipe Flow Pressure Dynamics
Pressure drop occurs as fluid flows through pipes due to friction between the fluid and pipe wall. This pressure drop must be overcome by pumps to maintain fluid flow. Pressure drop is caused by factors like friction and viscosity, and can be calculated using equations that consider pipe diameter, fluid properties, and flow characteristics like laminar or turbulent flow. Minor losses also contribute to pressure drop and can be estimated using resistance coefficients for components like sudden enlargements.
Uploaded by
Nixon RamsaranCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 42