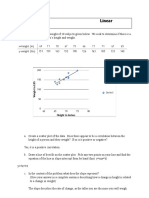
0% found this document useful (0 votes)
300 views18 pagesProbability Experiment: Toss Two Coins Toss Three Coins Roll Two Dice
Here are the steps to solve this problem:
a) The number of possible outcomes is 6 (from the die) x 2 (from the coin) = 12
b) See the tree diagram and tabular form representations below
c) P(five and Head) = 1/12
d) P(five or Head) = 7/12
e) P(even number and Tail) = 3/12
So in summary, the number of possible outcomes is 12, represented by the tree diagram and table. The probabilities of the specific events are 1/12, 7/12, and 3/12 respectively.
Uploaded by
rocklandgetCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
300 views18 pagesProbability Experiment: Toss Two Coins Toss Three Coins Roll Two Dice
Here are the steps to solve this problem:
a) The number of possible outcomes is 6 (from the die) x 2 (from the coin) = 12
b) See the tree diagram and tabular form representations below
c) P(five and Head) = 1/12
d) P(five or Head) = 7/12
e) P(even number and Tail) = 3/12
So in summary, the number of possible outcomes is 12, represented by the tree diagram and table. The probabilities of the specific events are 1/12, 7/12, and 3/12 respectively.
Uploaded by
rocklandgetCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 18