0% found this document useful (0 votes)
203 views34 pagesSupport Vector Machines: (Vapnik, 1979)
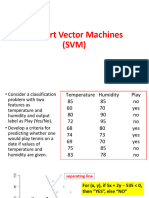
Support vector machines (SVMs) are a supervised learning method for classification and regression. SVMs find the optimal separating hyperplane that maximizes the margin between positive and negative examples. The hyperplane is defined by support vectors, which are the closest training examples to the hyperplane. SVMs can handle non-linearly separable data using kernel functions to map inputs to higher dimensions where a separating hyperplane may exist. Precision and recall are used to evaluate classifier performance, where precision measures the proportion of correct positive predictions and recall measures the proportion of actual positive examples that were correctly identified.
Uploaded by
sisda amaliaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
203 views34 pagesSupport Vector Machines: (Vapnik, 1979)
Support vector machines (SVMs) are a supervised learning method for classification and regression. SVMs find the optimal separating hyperplane that maximizes the margin between positive and negative examples. The hyperplane is defined by support vectors, which are the closest training examples to the hyperplane. SVMs can handle non-linearly separable data using kernel functions to map inputs to higher dimensions where a separating hyperplane may exist. Precision and recall are used to evaluate classifier performance, where precision measures the proportion of correct positive predictions and recall measures the proportion of actual positive examples that were correctly identified.
Uploaded by
sisda amaliaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 34