0% found this document useful (0 votes)
403 views4 pages1.arithmetic Sequence & Series
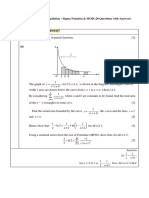
1. The document discusses arithmetic sequences and series, providing formulas and examples of problems involving finding terms, differences, and sums of arithmetic sequences and series.
2. One example asks to find the first term and common difference of a sequence given the second term is 7 and the sum of the first four terms is 12. Another example involves finding the number of terms less than 400 for a sequence with given first two terms.
3. The document also provides problems involving finding expressions for the nth term, sums of sequences, and common differences of sequences given additional information about terms or sums.
Uploaded by
Bhanupratap SisodiyaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
403 views4 pages1.arithmetic Sequence & Series
1. The document discusses arithmetic sequences and series, providing formulas and examples of problems involving finding terms, differences, and sums of arithmetic sequences and series.
2. One example asks to find the first term and common difference of a sequence given the second term is 7 and the sum of the first four terms is 12. Another example involves finding the number of terms less than 400 for a sequence with given first two terms.
3. The document also provides problems involving finding expressions for the nth term, sums of sequences, and common differences of sequences given additional information about terms or sums.
Uploaded by
Bhanupratap SisodiyaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 4