0% found this document useful (0 votes)
28 views25 pagesWeek4: (Chapter 4) Sorting Techniques: Given Suppose Suppose Goal
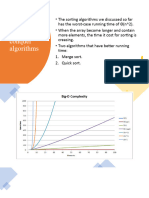
The document discusses various sorting techniques including bubble sort, insertion sort, selection sort, exchange sort, and quick sort. It provides descriptions of how each algorithm works and pseudocode examples. The key points covered are that bubble sort, insertion sort, selection sort, and exchange sort have O(n2) time complexity while quick sort has better O(n log n) time complexity on average but can degrade to O(n2) in worst case scenarios.
Uploaded by
Mhd BazziCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
28 views25 pagesWeek4: (Chapter 4) Sorting Techniques: Given Suppose Suppose Goal
The document discusses various sorting techniques including bubble sort, insertion sort, selection sort, exchange sort, and quick sort. It provides descriptions of how each algorithm works and pseudocode examples. The key points covered are that bubble sort, insertion sort, selection sort, and exchange sort have O(n2) time complexity while quick sort has better O(n log n) time complexity on average but can degrade to O(n2) in worst case scenarios.
Uploaded by
Mhd BazziCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 25