0% found this document useful (0 votes)
182 views4 pagesCompleting the Square Practice
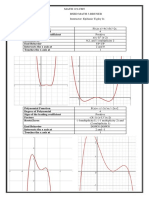
The document contains two activities on completing the square to solve quadratic equations:
1) Give the number that must be added to both sides of each equation to complete the square. There are 5 examples given.
2) Solve each equation by completing the square. The same 5 examples from Activity 1 are listed to be solved.
General instructions are given to complete additional exercises from the science textbook.
Uploaded by
Jayson Ryan LinoCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
182 views4 pagesCompleting the Square Practice
The document contains two activities on completing the square to solve quadratic equations:
1) Give the number that must be added to both sides of each equation to complete the square. There are 5 examples given.
2) Solve each equation by completing the square. The same 5 examples from Activity 1 are listed to be solved.
General instructions are given to complete additional exercises from the science textbook.
Uploaded by
Jayson Ryan LinoCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
/ 4