0% found this document useful (1 vote)
258 views8 pagesNumerical Analysis: MATLAB Practical (Autumn 2020) B.E. III Semester Thapar Institute of Engineering & Technology Patiala
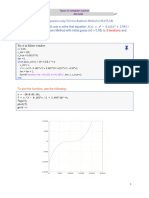
This document contains the solutions to various numerical analysis problems solved using MATLAB. It shows the MATLAB code used to apply the Newton-Raphson and secant methods to find the roots of nonlinear equations. For each problem, the code, inputs, outputs, and solutions are clearly displayed.
Uploaded by
Aarohan VermaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (1 vote)
258 views8 pagesNumerical Analysis: MATLAB Practical (Autumn 2020) B.E. III Semester Thapar Institute of Engineering & Technology Patiala
This document contains the solutions to various numerical analysis problems solved using MATLAB. It shows the MATLAB code used to apply the Newton-Raphson and secant methods to find the roots of nonlinear equations. For each problem, the code, inputs, outputs, and solutions are clearly displayed.
Uploaded by
Aarohan VermaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 8