50% found this document useful (2 votes)
353 views2 pagesEMI Class Notes Assignment 1
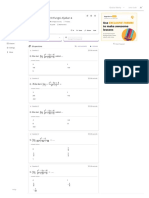
The document contains examples and solutions for calculating measurement errors and uncertainties for various electrical instruments. It discusses determining the resolution of a moving coil ammeter, limiting error percentages for ammeters and voltmeters, and calculating absolute and relative errors for measurements of resistance, capacitance, and power. The examples cover key concepts like full scale readings, scale divisions, percentage accuracy, and using measured values and errors to determine true values.
Uploaded by
Praneshvar PraneshvarCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
50% found this document useful (2 votes)
353 views2 pagesEMI Class Notes Assignment 1
The document contains examples and solutions for calculating measurement errors and uncertainties for various electrical instruments. It discusses determining the resolution of a moving coil ammeter, limiting error percentages for ammeters and voltmeters, and calculating absolute and relative errors for measurements of resistance, capacitance, and power. The examples cover key concepts like full scale readings, scale divisions, percentage accuracy, and using measured values and errors to determine true values.
Uploaded by
Praneshvar PraneshvarCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
/ 2