0% found this document useful (0 votes)
263 views5 pagesEEE211 Assignment 1
The document is an assignment for an electrical circuits course consisting of 4 problems. It provides expressions and diagrams related to sinusoidal voltages and currents, discusses phase differences, and calculates average and RMS values. The key points are:
1) It gives expressions for a voltage and current waveform and determines they are out of phase by 75 degrees with the current lagging the voltage.
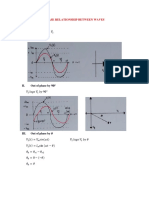
2) It writes expressions for waveforms shown in a figure and determines they are out of phase by 160 degrees with the voltage leading the current.
3) It finds the average value of half-circle and offset waveforms and determines the DC offset of one is 6V.
4) It calculates the RMS value of a voltage
Uploaded by
Samina TohfaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
263 views5 pagesEEE211 Assignment 1
The document is an assignment for an electrical circuits course consisting of 4 problems. It provides expressions and diagrams related to sinusoidal voltages and currents, discusses phase differences, and calculates average and RMS values. The key points are:
1) It gives expressions for a voltage and current waveform and determines they are out of phase by 75 degrees with the current lagging the voltage.
2) It writes expressions for waveforms shown in a figure and determines they are out of phase by 160 degrees with the voltage leading the current.
3) It finds the average value of half-circle and offset waveforms and determines the DC offset of one is 6V.
4) It calculates the RMS value of a voltage
Uploaded by
Samina TohfaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
/ 5