0% found this document useful (0 votes)
21 views45 pagesSignal Processing I 2020
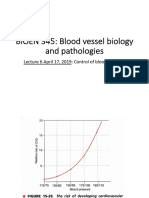
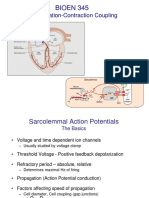
This document discusses signal processing techniques for analyzing neural data recorded from the brain. It begins with an overview of common neural recording methods like EEG, ECoG, and intracellular and extracellular recordings. It then discusses how frequency domain analysis techniques like the Fourier transform and discrete Fourier transform can be used to decompose neural signals into their frequency components to identify oscillations and fluctuations. Issues with Fourier analysis for non-stationary neural signals are noted. Wavelet analysis is introduced as an alternative approach. Examples are provided of using frequency features extracted from ECoG signals to control devices and of wavelet decomposition of EEG data. Spike sorting techniques for identifying individual neurons from extracellular recordings are also summarized.
Uploaded by
asdfghjklCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
21 views45 pagesSignal Processing I 2020
This document discusses signal processing techniques for analyzing neural data recorded from the brain. It begins with an overview of common neural recording methods like EEG, ECoG, and intracellular and extracellular recordings. It then discusses how frequency domain analysis techniques like the Fourier transform and discrete Fourier transform can be used to decompose neural signals into their frequency components to identify oscillations and fluctuations. Issues with Fourier analysis for non-stationary neural signals are noted. Wavelet analysis is introduced as an alternative approach. Examples are provided of using frequency features extracted from ECoG signals to control devices and of wavelet decomposition of EEG data. Spike sorting techniques for identifying individual neurons from extracellular recordings are also summarized.
Uploaded by
asdfghjklCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 45