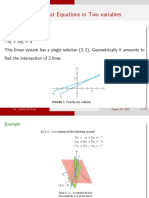
Sytem of linear equations

—————————————–

Phan Thi Khanh Van

E-mail: khanhvanphan@hcmut.edu.vn

September 18, 2018

(Phan Thi Khanh Van) System of linear equations September 18, 2018 1 / 14
Table of contents

1 System of linear equations

2 Cramer’s rule

3 The homogeneous system of linear equations

(Phan Thi Khanh Van) System of linear equations September 18, 2018 2 / 14
 System of linear equations

System of linear equations

System of m linear equations with n variables



 a11 x1 + a12 x2 + · · · + a1n xn = b1

a x + a x + · · · + a x = b
21 1 22 2 2n n 2


 ...

a x + a x + · · · + a x
m1 1 m2 2 mn n = bm
is rewritten
 as A.X = b 
a11 a12 . . . a1n b1
 a21 a22 . . . a2n b2 
(A|b) =   ... ... ... ...

... 
am1 am2 . . . amn bm

(Phan Thi Khanh Van) System of linear equations September 18, 2018 3 / 14
 Cramer’s rule

Cramer’s rule
Consider a system of n linear equations for n unknowns,
represented in matrix multiplication form as follows:
A.X = b (1) (square system). In case that System (1)
has a unique solution (⇔ det(A) 6= 0), the individual
det(Ai )
values for the unknowns are given by: xi = ,
det(A)
where Ai is the matrix formed by replacing the i−th
column of A by the column vector b.

(Phan Thi Khanh Van) System of linear equations September 18, 2018 4 / 14
 Cramer’s rule

Example
Check if the Cramer’s rule is applicable and if it is, solve
the following systems:
( (
x1 + x2 = 2 mx1 − x2 = −(m + 2)
1

x1 − 2x2 = 3 x1 + mx2 = m2 + 3
In R 3 find m such that
 4
 x 1 − x 2 − 2x 3 = 1
the following 3 planes :

2
x1 − x2 + x3 = −1
 x + my + z = 1, 2x + y −
2x1 − 3x2 + 4x3 = 2

z = 3, 3x + y + mz = −3
3 are concurrent.

(Phan Thi Khanh Van) System of linear equations September 18, 2018 5 / 14
 Cramer’s rule

Kronecker-Capelli theorem
The system of linear equations Ax = b, A ∈ Mm×n is
compatible iff r (A) = r (A|b).
r (A) < r (A|b): there is no solution.
r (A) = r (A|b) = n: the solution is unique.
r (A) = r (A|b) = r < n: there is an infinite number of
solutions
Gauss-Jordan elimination (row reduction)
1 (A|b) elem. row operations echelon form.
−−−−−−−−−−−−−−→
2 From r (A), r (A|b) derive the number of solutions.
3 Find the reduced row echelon form and solve the
variables in the reverse order.
(Phan Thi Khanh Van) System of linear equations September 18, 2018 6 / 14
 Cramer’s rule

Example
Solve the following systems
 3
x1 + x2 − 3x3 = 3
 
2x1 + x2 − 3x3 + x4 = 3
x1 − x2 + x3 = −1
1



x − x + x + x = −1
1 2 3 4

3x − x2 − x3 = 5

 1 −2x2 + x4 = 0
x1 − x2 − 2x3 = 1
 


 
4x − x − x + 3x = 1

x − x + x = −1 1 2 3 4
1 2 3
2



 x1 − 2x2 + x3 = 2

3x − 3x = 2
1 2

(Phan Thi Khanh Van) System of linear equations September 18, 2018 7 / 14
 The homogeneous system of linear equations

The homogeneous system of linear equations

A.X = 0
.
Remark: The homogeneous system has the trivial
solution x = (0, 0...0)

(Phan Thi Khanh Van) System of linear equations September 18, 2018 8 / 14
 The homogeneous system of linear equations

Example

x1 − x2 − 2x3 + x4 = 0

Solve the system 2x1 − 2x2 + x3 − x4 = 0

4x1 − 4x2 − 3x3 + x4 = 0

   
1 −1 −2 1 0 1 −1 −2 1 0
 2 −2 1 −1 0  →  0 0 5 −3 0 
4 −4 −3 1 0 0 0 5 −3 0
 
1 −1 −2 1 0
→ 0 0 5 −3 0  There is an infinite number
0 0 0( 0 0
x2 = α
of solutions ⇒
x4 = β
(
(Phan Thi Khanh Van) System of linear equations September 18, 2018 9 / 14
 The homogeneous system of linear equations

Properties of the homogeneous system of linear

equations
Given A.X = 0.
r (A) = n: The trivial solution is the unique solution
r (A) < n: There is an infinite number of solutions
(there are non trivial solutions).
Given the homogeneous system of n linear equations with
n variables.
det(A) 6= 0: the trivial solution is the unique solution.
det(A) = 0: there is an infinite number of solutions.

(Phan Thi Khanh Van) System of linear equations September 18, 2018 10 / 14
 The homogeneous system of linear equations

Example
Find
 m such that the system has a unique solution:
x1 + 2x2 − x3 = 0

mx1 − x2 + x3 = 0

x2 − mx3 = 0

 
1 2 −1
A = m −1 1 
0 1 −m
The system has a unique solution ⇔ det(A) 6= 0
⇔ −m(−1 − 2m) − 1(1 + m) 6= 0
⇔ 2m2 6= 1 ⇔ m 6= ± √12

(Phan Thi Khanh Van) System of linear equations September 18, 2018 11 / 14
 The homogeneous system of linear equations

Example
Find
 m such that the system has nontrivial solutions:


 mx1 + x2 + x3 + x4 = 0

x + mx + x + x = 0
1 2 3 4


 x1 + x2 + mx3 + x4 = 0

x + x + x + mx = 0
1 2 3 4
 
m 1 1 1 
 
1 m 1 1
The system has nontrivial solutions ⇔  =0
 1 1 m 1 

 1 1 1 m

(Phan Thi Khanh Van) System of linear equations September 18, 2018 12 / 14
 The homogeneous system of linear equations

 
1 1 1 1 
 
1 m 1 1 
⇔ (m + 3)  =0
 1 1 m 1 

1 1 1 m 
 
1 1 1 1 
 
0 m − 1 0 0 
⇔ (m + 3)  =0
 0 0 m − 1 0 

0 0 0 m − 1
⇔ (m + 3)(m − 1)3 = 0 ⇔ m = −3 ∨ m = 1

(Phan Thi Khanh Van) System of linear equations September 18, 2018 13 / 14
 The homogeneous system of linear equations

Thank you for your attention!

(Phan Thi Khanh Van) System of linear equations September 18, 2018 14 / 14