100% found this document useful (2 votes)
3K views48 pagesSection 5 - Triangles - Part 1 Answer Key
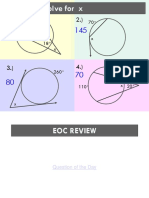
1) The document provides information about classifying and proving properties of triangles. It discusses triangle angles, sides, congruence, and using coordinates.
2) Key concepts covered include the three types of triangles based on angles (acute, obtuse, right), triangle congruence postulates (SSS, SAS, ASA, AAS), finding triangle area and perimeter with coordinates, and using triangle congruency to solve for missing variables.
3) The document contains examples and practice problems for readers to apply triangle concepts and properties.
Uploaded by
Erryn LoweCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
100% found this document useful (2 votes)
3K views48 pagesSection 5 - Triangles - Part 1 Answer Key
1) The document provides information about classifying and proving properties of triangles. It discusses triangle angles, sides, congruence, and using coordinates.
2) Key concepts covered include the three types of triangles based on angles (acute, obtuse, right), triangle congruence postulates (SSS, SAS, ASA, AAS), finding triangle area and perimeter with coordinates, and using triangle congruency to solve for missing variables.
3) The document contains examples and practice problems for readers to apply triangle concepts and properties.
Uploaded by
Erryn LoweCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 48