0% found this document useful (0 votes)
59 views15 pagesSolid Dynamics - Lecture 6: Moments of Inertia
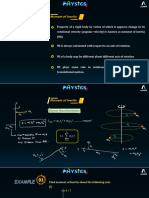
This document discusses moments of inertia, including:
1) Moments of inertia for a system of material points with respect to different axes.
2) Products of inertia with respect to axes.
3) Moments and products of inertia with respect to parallel axes using Steiner's theorem.
4) Moments of inertia for basic shapes like rods, discs, rectangular solids, and spheres.
Uploaded by
Anna LoveCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
59 views15 pagesSolid Dynamics - Lecture 6: Moments of Inertia
This document discusses moments of inertia, including:
1) Moments of inertia for a system of material points with respect to different axes.
2) Products of inertia with respect to axes.
3) Moments and products of inertia with respect to parallel axes using Steiner's theorem.
4) Moments of inertia for basic shapes like rods, discs, rectangular solids, and spheres.
Uploaded by
Anna LoveCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 15