0% found this document useful (0 votes)
55 views7 pagesDigital Signal Processing Laboratory Examination: Punit Kumar Ojha 18EE01011
The document summarizes two digital signal processing experiments:
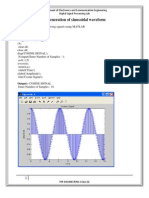
1) Design of a digital sinusoidal oscillator with a frequency of 100 Hz and amplitude of 2 using a sampling rate of 1000 Hz. The experiment results in a frequency error of 2 Hz.
2) Design of a digital DTMF transmitter and receiver to transmit and receive the number 7. The experiment generates tones at 850 Hz and 1210 Hz with frequency errors of 2 Hz and 1 Hz respectively.
Uploaded by
Punit OjhaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
55 views7 pagesDigital Signal Processing Laboratory Examination: Punit Kumar Ojha 18EE01011
The document summarizes two digital signal processing experiments:
1) Design of a digital sinusoidal oscillator with a frequency of 100 Hz and amplitude of 2 using a sampling rate of 1000 Hz. The experiment results in a frequency error of 2 Hz.
2) Design of a digital DTMF transmitter and receiver to transmit and receive the number 7. The experiment generates tones at 850 Hz and 1210 Hz with frequency errors of 2 Hz and 1 Hz respectively.
Uploaded by
Punit OjhaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 7