0% found this document useful (0 votes)
82 views2 pagesTrigonometric Ratios in Right Triangles
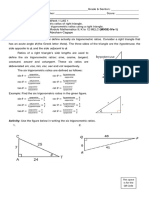
This document provides information about trigonometric ratios and examples of calculating trigonometric ratios in right triangles. It defines the six trigonometric ratios - sine, cosine, tangent, cosecant, secant, and cotangent - and provides their formulas in terms of the opposite, adjacent, and hypotenuse sides of a right triangle. It then works through two examples, calculating the trigonometric ratios of given angles using the information provided about the sides of right triangles. The document concludes by providing an activity for students to find the six trigonometric ratios of a given angle in another right triangle.
Uploaded by
Jessa Lou Liba CapapasCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
82 views2 pagesTrigonometric Ratios in Right Triangles
This document provides information about trigonometric ratios and examples of calculating trigonometric ratios in right triangles. It defines the six trigonometric ratios - sine, cosine, tangent, cosecant, secant, and cotangent - and provides their formulas in terms of the opposite, adjacent, and hypotenuse sides of a right triangle. It then works through two examples, calculating the trigonometric ratios of given angles using the information provided about the sides of right triangles. The document concludes by providing an activity for students to find the six trigonometric ratios of a given angle in another right triangle.
Uploaded by
Jessa Lou Liba CapapasCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
/ 2