0% found this document useful (0 votes)
249 views21 pagesThe SIMPLE Algorithm For Pressure-Velocity Coupling
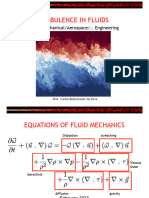
This document discusses the SIMPLE algorithm, which is a classic segregated solution method for solving incompressible flow problems. It begins by providing an overview of structured versus unstructured meshes and staggered grids. It then describes the basic discretization of the momentum and continuity equations on a staggered grid, resulting in a coupled system of equations. However, the SIMPLE algorithm instead solves this system sequentially in a segregated manner by separately solving for the velocity, pressure, and other fields in an iterative approach.
Uploaded by
kushal bosuCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
249 views21 pagesThe SIMPLE Algorithm For Pressure-Velocity Coupling
This document discusses the SIMPLE algorithm, which is a classic segregated solution method for solving incompressible flow problems. It begins by providing an overview of structured versus unstructured meshes and staggered grids. It then describes the basic discretization of the momentum and continuity equations on a staggered grid, resulting in a coupled system of equations. However, the SIMPLE algorithm instead solves this system sequentially in a segregated manner by separately solving for the velocity, pressure, and other fields in an iterative approach.
Uploaded by
kushal bosuCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 21