0% found this document useful (0 votes)
222 views13 pagesPSAT Math Practice Test: Passport To Advanced Math - Functions
1. The document contains a practice test for the PSAT Math section covering functions. Question 1 asks which list could represent the domain of a function modeling the number of fish eggs laid over time. The correct answer is the list containing only whole numbers greater than or equal to 0.
2. Question 2 asks the value of evaluating one function at 5 and subtracting it from evaluating the same function at 2. The correct answer is 9.
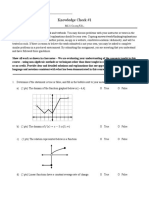
3. Question 3 asks which statement about a quadratic function graph is not true. The correct statement is that the function does not equal 4 when the input is 2.
This summarizes the context and key details from the first 3 questions in the PSAT Math practice test
Uploaded by
Mariluz TorresCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
222 views13 pagesPSAT Math Practice Test: Passport To Advanced Math - Functions
1. The document contains a practice test for the PSAT Math section covering functions. Question 1 asks which list could represent the domain of a function modeling the number of fish eggs laid over time. The correct answer is the list containing only whole numbers greater than or equal to 0.
2. Question 2 asks the value of evaluating one function at 5 and subtracting it from evaluating the same function at 2. The correct answer is 9.
3. Question 3 asks which statement about a quadratic function graph is not true. The correct statement is that the function does not equal 4 when the input is 2.
This summarizes the context and key details from the first 3 questions in the PSAT Math practice test
Uploaded by
Mariluz TorresCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 13