0% found this document useful (0 votes)
241 views5 pagesGEC3 Assignment 5 PDF
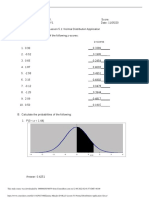
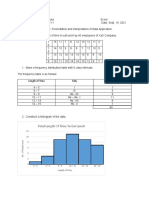
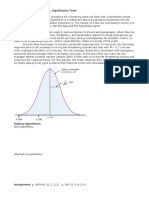
This document contains an assignment with multiple questions on probability and statistics concepts like the normal distribution and linear regression. For each question, the student provided calculations and answers. The questions involve finding probabilities for normal random variables, determining the percentage of students below a GPA, calculating the mean and standard deviation from given probabilities, finding the probability of an event occurring after a given number of days, and analyzing the relationship between distance and fuel usage through scatter plots, correlation, regression lines, and variability.
Uploaded by
Bhebz Erin MaeCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
241 views5 pagesGEC3 Assignment 5 PDF
This document contains an assignment with multiple questions on probability and statistics concepts like the normal distribution and linear regression. For each question, the student provided calculations and answers. The questions involve finding probabilities for normal random variables, determining the percentage of students below a GPA, calculating the mean and standard deviation from given probabilities, finding the probability of an event occurring after a given number of days, and analyzing the relationship between distance and fuel usage through scatter plots, correlation, regression lines, and variability.
Uploaded by
Bhebz Erin MaeCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 5