0% found this document useful (0 votes)
96 views25 pages11-Simple Linear Regression
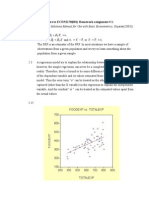
The document describes simple linear regression. Simple linear regression is used to predict a dependent variable (Y) based on an independent variable (X). It generates a regression equation of the form Y = βX + α, where β is the slope and α is the intercept. Residual plots are examined to check if the data meets the assumptions of linearity, normality and homoscedasticity. An example uses data to predict academic score based on number of free meals and checks if the assumptions are met before conducting the linear regression analysis. The results show number of free meals significantly predicts academic score and explains about 67% of variance in academic scores.
Uploaded by
MUHAMMAD AZRAI MOHD ZUNAIDICopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
96 views25 pages11-Simple Linear Regression
The document describes simple linear regression. Simple linear regression is used to predict a dependent variable (Y) based on an independent variable (X). It generates a regression equation of the form Y = βX + α, where β is the slope and α is the intercept. Residual plots are examined to check if the data meets the assumptions of linearity, normality and homoscedasticity. An example uses data to predict academic score based on number of free meals and checks if the assumptions are met before conducting the linear regression analysis. The results show number of free meals significantly predicts academic score and explains about 67% of variance in academic scores.
Uploaded by
MUHAMMAD AZRAI MOHD ZUNAIDICopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 25