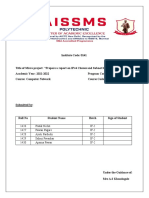
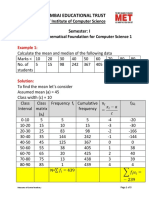
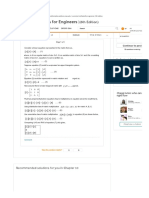
0% found this document useful (0 votes)
106 views8 pages2nd Lecture
The document describes the Hill cipher, which uses matrix multiplication and modulo arithmetic for encryption. The key is a matrix with an inverse modulo 26. To encrypt, plaintext letters are represented as numerical values and multiplied by the key matrix. Decryption uses the inverse key matrix. Examples are provided to illustrate encrypting and decrypting text using 2x2 and 3x3 key matrices. Finding the inverse matrix, determinant, and adjugate are important steps in decryption. The document also provides an example of determining the encryption key given plaintext and ciphertext.
Uploaded by
AHMED DARAJCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
106 views8 pages2nd Lecture
The document describes the Hill cipher, which uses matrix multiplication and modulo arithmetic for encryption. The key is a matrix with an inverse modulo 26. To encrypt, plaintext letters are represented as numerical values and multiplied by the key matrix. Decryption uses the inverse key matrix. Examples are provided to illustrate encrypting and decrypting text using 2x2 and 3x3 key matrices. Finding the inverse matrix, determinant, and adjugate are important steps in decryption. The document also provides an example of determining the encryption key given plaintext and ciphertext.
Uploaded by
AHMED DARAJCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 8