0% found this document useful (0 votes)
159 views15 pagesCore Data Analysis Worksheet 9-Ex4DE
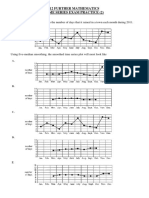
1. The document contains 10 multiple choice questions about time series analysis and seasonal adjustment.
2. The questions cover topics such as identifying seasonal indices, calculating deseasonalized values, interpreting trends in time series data, and smoothing time series data using moving averages.
3. Many of the questions provide tables of seasonal indices or time series data and ask students to analyze the patterns, calculate values, or choose the best multiple choice answer about the data presented.
Uploaded by
chris brownCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
159 views15 pagesCore Data Analysis Worksheet 9-Ex4DE
1. The document contains 10 multiple choice questions about time series analysis and seasonal adjustment.
2. The questions cover topics such as identifying seasonal indices, calculating deseasonalized values, interpreting trends in time series data, and smoothing time series data using moving averages.
3. Many of the questions provide tables of seasonal indices or time series data and ask students to analyze the patterns, calculate values, or choose the best multiple choice answer about the data presented.
Uploaded by
chris brownCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 15