0% found this document useful (0 votes)
35 views50 pagesChap4 Slides
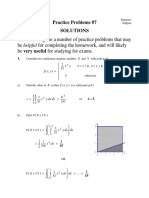
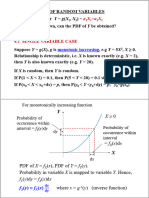
The document discusses joint probability distributions of discrete and continuous bivariate random variables. It defines joint and marginal density functions, independent random variables, expectation, covariance, and provides examples to illustrate these concepts.
Uploaded by
Parv SojatiaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
35 views50 pagesChap4 Slides
The document discusses joint probability distributions of discrete and continuous bivariate random variables. It defines joint and marginal density functions, independent random variables, expectation, covariance, and provides examples to illustrate these concepts.
Uploaded by
Parv SojatiaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 50