0% found this document useful (0 votes)
34 views23 pagesAc Current
The document discusses alternating current (AC) and how it differs from direct current (DC). It provides key points about AC:
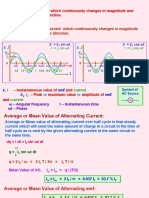
- AC voltage and current vary sinusoidally over time, represented by rotating vectors called phasors.
- When AC is applied to a resistor, the voltage and current are in phase. When applied to an inductor, the current lags the voltage by 90 degrees. When applied to a capacitor, the current leads the voltage by 90 degrees.
- Root mean square (RMS) values are used to calculate power in AC circuits, analogous to using voltage and current in DC circuits. RMS voltage or current is the equivalent DC value that would produce the same power dissipation
Uploaded by
midhunesh41Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
34 views23 pagesAc Current
The document discusses alternating current (AC) and how it differs from direct current (DC). It provides key points about AC:
- AC voltage and current vary sinusoidally over time, represented by rotating vectors called phasors.
- When AC is applied to a resistor, the voltage and current are in phase. When applied to an inductor, the current lags the voltage by 90 degrees. When applied to a capacitor, the current leads the voltage by 90 degrees.
- Root mean square (RMS) values are used to calculate power in AC circuits, analogous to using voltage and current in DC circuits. RMS voltage or current is the equivalent DC value that would produce the same power dissipation
Uploaded by
midhunesh41Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 23