0% found this document useful (0 votes)
73 views40 pagesModule I Complete
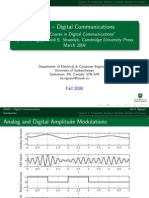
- The document discusses signals and spectra, with advantages and disadvantages of digital communications. It introduces source coding which converts analog signals to digital bits.
- It covers sampling and quantization, with the sampling theorem stating a signal can be represented if the sampling frequency is at least twice the highest frequency. For a given signal, quantization to 9 levels allowed mapping to binary digits.
- Classification of signals is discussed, including deterministic vs random signals. Probability theory is introduced for analyzing random signals. Basic probability terms and properties are defined.
Uploaded by
jigef19343Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
73 views40 pagesModule I Complete
- The document discusses signals and spectra, with advantages and disadvantages of digital communications. It introduces source coding which converts analog signals to digital bits.
- It covers sampling and quantization, with the sampling theorem stating a signal can be represented if the sampling frequency is at least twice the highest frequency. For a given signal, quantization to 9 levels allowed mapping to binary digits.
- Classification of signals is discussed, including deterministic vs random signals. Probability theory is introduced for analyzing random signals. Basic probability terms and properties are defined.
Uploaded by
jigef19343Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 40