0% found this document useful (0 votes)
40 views35 pagesPSK Techniques for Engineers
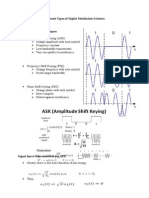
Phase Shift Keying (PSK) is a digital modulation technique where the phase of the carrier signal is shifted according to the input data. There are two main types: BPSK uses two phases that are 0° and 180°, while QPSK uses four phases that are 0°, 90°, 180°, and 270°. PSK is widely used in wireless technologies due to its robustness to noise compared to amplitude-based modulation. It allows higher data rates or improved noise immunity compared to BPSK.
Uploaded by
HarishCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
40 views35 pagesPSK Techniques for Engineers
Phase Shift Keying (PSK) is a digital modulation technique where the phase of the carrier signal is shifted according to the input data. There are two main types: BPSK uses two phases that are 0° and 180°, while QPSK uses four phases that are 0°, 90°, 180°, and 270°. PSK is widely used in wireless technologies due to its robustness to noise compared to amplitude-based modulation. It allows higher data rates or improved noise immunity compared to BPSK.
Uploaded by
HarishCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 35