0% found this document useful (0 votes)
221 views4 pagesTransformations of Linear Functions
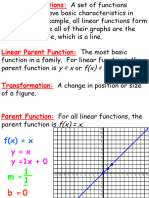
The document discusses transformations of linear functions. It explains how changing the parent function f(x)=x by adding or subtracting values, multiplying the function or input values by constants, or shifting the function horizontally affects the slope, y-intercept, and graph of the transformed function.
Uploaded by
Tyler LopezCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
221 views4 pagesTransformations of Linear Functions
The document discusses transformations of linear functions. It explains how changing the parent function f(x)=x by adding or subtracting values, multiplying the function or input values by constants, or shifting the function horizontally affects the slope, y-intercept, and graph of the transformed function.
Uploaded by
Tyler LopezCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 4