0% found this document useful (0 votes)
89 views11 pagesClosed Loop Systems
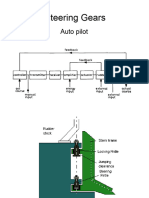
This document provides an overview of closed loop control systems. It discusses key concepts like the plant, controlling and measured parameters, feedback, error signals, and gain. Examples of closed loop systems include home heating/AC, vehicle speed control, and aircraft autopilot. Proportional, integral and derivative control methods are introduced. The complexity of modeling non-linear systems using differential equations is also covered. The goal of closed loop control is to provide stable, fast responses to transients and restore the measured parameter following a disturbance.
Uploaded by
Mohamed RashidCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
89 views11 pagesClosed Loop Systems
This document provides an overview of closed loop control systems. It discusses key concepts like the plant, controlling and measured parameters, feedback, error signals, and gain. Examples of closed loop systems include home heating/AC, vehicle speed control, and aircraft autopilot. Proportional, integral and derivative control methods are introduced. The complexity of modeling non-linear systems using differential equations is also covered. The goal of closed loop control is to provide stable, fast responses to transients and restore the measured parameter following a disturbance.
Uploaded by
Mohamed RashidCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 11