0% found this document useful (0 votes)
34 views18 pagesLecture7 8
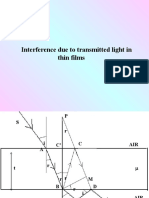
1) Interference occurs when light rays reflect off the top and bottom surfaces of a thin transparent film, with the reflected rays interfering with each other. 2) The path difference between these reflected rays depends on the thickness of the film and the angle of incidence. 3) For maximum (bright fringe) interference, the path difference must be equal to an integer multiple of the wavelength, and for minimum (dark fringe) interference the path difference must be an odd integer plus one-half of the wavelength.
Uploaded by
Rajan ThakurCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
34 views18 pagesLecture7 8
1) Interference occurs when light rays reflect off the top and bottom surfaces of a thin transparent film, with the reflected rays interfering with each other. 2) The path difference between these reflected rays depends on the thickness of the film and the angle of incidence. 3) For maximum (bright fringe) interference, the path difference must be equal to an integer multiple of the wavelength, and for minimum (dark fringe) interference the path difference must be an odd integer plus one-half of the wavelength.
Uploaded by
Rajan ThakurCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 18