0% found this document useful (0 votes)
36 views18 pagesLecture 2
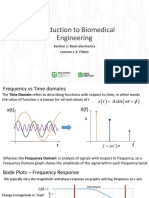
The document discusses transfer functions and their analysis in the s-domain. It covers common source amplifiers, Miller's theorem, poles and zeros, and bode plots. Bode plots can be used to analyze the magnitude and phase response of a transfer function. The document also discusses the low frequency, mid-band, and high frequency behavior of amplifier transfer functions. Key aspects covered include the dominant pole approximation and estimating corner frequencies from poles and zeros.
Uploaded by
Nimsiri AbhayasingheCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
36 views18 pagesLecture 2
The document discusses transfer functions and their analysis in the s-domain. It covers common source amplifiers, Miller's theorem, poles and zeros, and bode plots. Bode plots can be used to analyze the magnitude and phase response of a transfer function. The document also discusses the low frequency, mid-band, and high frequency behavior of amplifier transfer functions. Key aspects covered include the dominant pole approximation and estimating corner frequencies from poles and zeros.
Uploaded by
Nimsiri AbhayasingheCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 18