TOPIC! 2 FUNCTIONS “i 4 Z1/- Straight Lines Mee # Strnight Lines moy be drawn with a graph of a linear fienction. The fom that you have probably seen the most tn previous uears is y=muctc : Y=Moc+C/h This is the gradient - intercept form, and m&C tel us certain properties aout ee Vinee zc changes, y changes by fuer! &. gradients = 32 = BEE =M. So m is the gradient /slope. If you tren sot x=0 in any function, you can find y-tnborcepts. In any y=mx+c, a Yyomle)#e , $0 we & a ypinbereepe, E.G.4 fr draw a groph — Gendent = 2. (= 5) 1A Of function: y= 2x-~ 1 ap gat ax+by+d=0/4 Tis i another cometon form for a stright Line, ard We. oan derive ib from: y= mare “=> -mx+y-c=0, then if m isa fraction, we can sukiply everything by the denominator bo get integer coefficients. ©.6.2 Pr Express yo-2sX+u in the fom: axtoysd=0 (a,beZ) Ltgasy-uo 2+ 2xr3y-12=0 : Y-Y = (X-2,) JP Wis more of a helpful: starting point for finding the eqation if you have. a. point (x,,y,) & a gradient (m). As m=43=9% we opt y-ycor(t-x), £.6.3/A Find equation of a line which is parallel to Y= 2x-3, passing Yroudn (2,3) : Luce YY, = m(2c~20,) —> 4-3 = 2(e- ) y- “322-2 Y= Deed PERPENDICULAR > IF we voant: to go from a slope of one Line to the slepe of a perpendicular line, then ik must change from: fI5—> WE or [On —> ab | €.G. t+ Find og, of a Line perpendicular to y=%x-lr, passing Unrough (40, -3): L, Slope 8g “Bs Ag = Ae, Yo-Yo (26-0) 9 Yt = 2B (x-10) > y= For H] INTERSECTIONS /+ Two Lines? intersection poink con be found by “setking them equal tp each other’, which is esseubially just substitution, £.6,5 + Find the intersection point ef y=2x-1@ y=-x+8 L soe “Hr BaIxe-], Wade, x=S. Plug-in: y=213)-1 > y=5 ~. (3,5)[2.2/- Function Concepts “fel JP h function & a series of operations that will transform — MLW |v an, x value inko one specific (y) value. NOTATION/H The tuo main versions of writing a function will be: y=4x-3 or f(X)=4x-3. This takes aay x volue, multiplies ik +, and subtracts 3. For example , F(2)=4(2)-3=5. But, as usual , you may use any Letters for variables , such og a ‘Velociby-time’ function like vit) = 3t*+ Ze. Domain /eAnce|'> An important detail about functions is Knowing what set of X values You are able to plug in- the domacn, and which y values are possible bo get ouk of the funchion - the range. The things that may restrict the domain tnduide that: you con't divide by zero, you ‘can't do! the square root of a negotive , and you can’t do a log f O or a negative. The range. essentially hos an inverse set of restrictions, €.6.1/+Find the domain of F(x)= ln (x4): es hove 4+1>0 2. D>-4 artemate notation + {xe R|x>-1} E.c.2 J Find tne range of g(x)= 22%-3 : bas xO for any x, g(xe-3 Inverse/> We have seen how a regular function tums x's into y’s. The inverse of a function tums those y values back into thecr respective a values, reversing the opertions, To find these , we can switch x2y, then make y the subject again. Then write ik with the notation: $'@) =linverse funchion] £.G.3 Pr teg2ee%, gid f) E 6.6 hie}= ln), find, nil “bu canrigiagh af west a2 y=2e* b'@)= 2e* | funckion by reflecting the yadeel | bu=ln&) eee oe switeh xby | switch ray | orginal in tre Wine + ya 7 wely rh 1 x=tn&) ' 4 FY at v 1 toe mise power fe! cA x-l= 2y 1 =e ! 1 simplify | | Sah 1 ; \ I 1~ key Features of Graphs ee Lid dh You may well be asked to dius or sketch the graphs of Mt functions. Drawing Should be as accurate os possible, including all relevant gfoph features. Sketching should just give a general idea of the shape, with some features, depending on how He question is phrased, and what type of function & asked for. FEATURES Here we can define the jain tupes of graph features : Moxinus/ Minimum values /> Timing points’ of tne grog: as « Intercepts b Uonere the gmnph crosses tre x-axis or the y-axis, . Line of syrmetry A> Mainly reganling quodsatics , self-explanatory / Vertex /> Mox. or in. points for quadratic function. eles, toots/> Where y=O, i.e.: Une 2c-intercepts, Asymptotes > A Line that a graph will get infinitely close to but will never touch, as the x or y tends to infinity. Intersection points fr The potat where {wo Lines cross (intersect), FeaTURes on A GRarH/> To visualise the above features : fin, Hottzontal Y L, Represented by a dood Line, labelled with, t& equation, SDC F>B graph almost any function, we press : T= nspive > CLGeArH) —> GAS) —> type function —> ESTED) Ti -suif> CE) type function —> GearL227 continued FINPING FEATURES »/ GDC //> You can find the features previously defined by wsing your GDC's ‘oaolyse graph’ capabilities : Ti-sspire > GID) — CHADANSE GMD... f/ 71-344» CD ERD... FINDING FeaTuRes/+ We can Find many of these: manuolly > Taming Points > You can use cateulus (see tepic L57), or for quadratics , you con use x= fa (see 2G for Aka, ZR for Au), otherwise use a GDC. [? intercepts Fo To be on the Y-axis, you must have X=0, se if you plag in x=0, | and solve for y, you have the y-intercept:. Reverse tints for x-intercept). Zeros & Roots / hopin, set y=0, and selwe. Vertical Asumptotes + At on zc value of rectricted domain, such as the 2 value that means upu would be dividing by 0. Horizontal Asymptotes > To find what value. the grag gets closer and closer to, Ge can plug it very lage values for x. Or use advanced calculus (Limits). Intersection Points fs Seo ZI (sek funckions equal to each ether, and solve) E.G. 1 Fe Draw the oagh of fc) == =Aytl: Divide by zero when x1, 50 VA. ab 2c=4 fs x-r00, fK)=O+l=1, so HA. ot x21 Plug in me Mieke at (0,-1) Set fx}=0: O= B41 axe-l, x-ink, at (4,0) £.6.2)/ Draw the graph of f(x)=x*-3x% + : yint. ak f(@\=0-044=4 yin. at (0,4) x-inks,: 8-324+4- 09 (xix-2ino, x=-182. “Taming points : GDC, or calculus : F(x) =3x-61=0, x=0K2 E.G. 3/F Draw the graph of aix)=2e* : Set x=0: )=2e"= D1=2 + yr int. ak (0,2) O=2e™ has no real solutions , so no x~int, fs x00 , a(x) 00, but as L- 09, 9)0 “HAL ak 220 =[2:5] Ties ¢ function MODELUNGI> We are going to cover many types oF Function tn Has a séchion, So that we. will have all. the, tools for the. process of modelling. This means ue twill: be able. to assign 0. function to a. real -vierid situakion . LINEAR FUNCTIONS > This © in the form: Yate or yaaxth We will refer to the former here. Eee Eee wita certain Features : t FEATURES |G i [E.@ lL Graph y=3a-2: RuLaBEceREE E15.) Dig hE ae (,-2), ~_tslope-b te "et | slope of 3 1 | T i is i 1 fx)aocce: QUADRATICS/> These are funcions in the form: f(x)=arts bec. Der Tt takes. one of {ne shapes. shown.on. Uke. righk ere + —> FEATURES > Eb 2bG x = =inbercegelo a (6,2) He >» Graph F(x) =x%4 2-2: Et | ttt a | >y-int. ak (0,-8) a ea ape a Ee 1 As of Syn dbase “ BNertexE ak (GE GR) 7 5 —PNertex Ps at (i, ta) 1 re LED » Xe thts.jrooks/zeresf> Can be Found Ly: co __F By factoring ak eu Fi CoE eT L ec faal Pfu GPC, ence Fuackion hos been graphed: Uy GDC er Factoring: (riw\ix-2) “|| “[-tooks are ok Cujo) “Ti-nspire Pp (EN > GrRwACTEE Gear + Bolu) IE ZERA) Choose: lower & upper bound | (ENTER) > Rect given ____ ET) -s6b td) Gi) Tizer9) ‘> Choose. Lefi.B right bound — Sere ereSaale ips are functions in the form Necktie 4 This is [cll increasing , asx (the. exponent) increases. This exponent can often represent Give (con be t, nok 2). This. is relevant Mee ee pt hie certnin percentage each year — in taal case , ' would stand for years [FEATURES /> [rr Pret 6.8. oF Grog. fe) =2371 » Shope For kz0.k a> 20, aliiys VARIATIONSI+£ (0) = fad= ke +c also has the same features, buk grows faster as increases. FAhese functions are highty relevant to any kind of grout % decay, geometric. “sequences and mote. (Je will see hot to Model Hasse in L2G) DIRECT VARIATION + This can, bea. Ltear, qadmbac or other polynomial, bub it only, contains the. lighest degree tem, such as flx)= 22 or Vl)=Wilr?. ‘The second example Hagre 420s. the volume of a sphere, bul can be. thougul of as slrowing heao, ved Seep LE apr in tae radius,continued (3/3) CUBIC MODELS These are functions wn the form: fac) =a2°4 bate cx+d You often just: see! these in the form..y Sax? tn ART SL Hough. You won't neeil to Keows ew to giaph these ats pea in detail, buk borieGly | They will have Une shape , such as > So oe NAL Other features include Hre fack that Hae. y-inkercept 18. at (0,d)_ You. maiy see. these used in many different fields, buk volume ts a Common one. For example, volume of a sphere: V=%% Ilr?) | SINUSOIDAL MoveLS F This could easily be moved to your shudies of Topic 3 if needed... 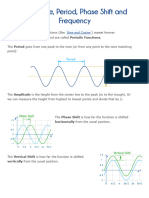Buk here is tae basic knowledge for Huse models : iGRarHs/b| | Pepitude =| Wes) “vel et taal ISo they are defined by theic principal axis, arplétude & peried — winich are y20., 1, and 211 respeckively for both base functions. They differ with a horizontal shift, with. y=sinx passing the origin (0,0), and. y= cosa. passing (0, 1) Now we’ can apply transformations such as afl), flex) & fod +d to trese - fuaccions. These. stretch the waves vectically, heizerta., cand shift vertically RULES + | [al = amplitude Gkp y=dsen(Ex)-3 iE y=asin(bx)+d | 2 = period A sine curve with, an a | Principal axis ak y=d | | amplitude of 2 { Tk has a principal axis af y=3_ + 1 tod ts BL-ZE Y= acos(bx)id I eae ele Period ts MlaAm ay | |ag Melling He HH a ‘ok les us_to truly aadertand 64 world psa. te fala fe alRiadeal (model) thok fits ond makes cha for the situakion, and Hues using ik be find out: various. inforwakion Tt requires plenty of evaluakion & critical refleckion Phocess [b This. an explanation & the process flow-chart that He 16 gives for modelling. Li Feo] Ee This will most. Likely be. pesed. fo you in.an exam. You ecan-wompi | | | | | i) pe eM propem | Moy pose_ pure ‘own problem tn an TA (er in cea ae {TT Oe PEVELOF OB Thee will usually be clues’ in Exo! question for uiaak _|- Limon bye of wodall & noedad. If sometlaing is added Try Rta] penédically, tren ib will be linear. Increasing by a % — Ab is etpenential. Cyclical? Maybe sinuscdal. Ind so on... ae {[feindl Uae carted conshaals i Oba plesticn fois inko’ Hao model. “Tesk ik. Accept or rejeck os appropriake. --H peer | IP Draw your graph, of plug sometining into, jper model, ty | TT | ope. {ileal aster Hh pedi a Hal | extesp | fee ia Hp et et fae ae oP | ___generalisakions. TE may need a tex model, so rebum to step 2. pay “per Film’, where Hoe {* film costs $1, Hien $2.50 per Hl A subscription model —cweks._an ee ea, Uren $3 per month. @) Creake. a. Tisear modal fee Hee Habe feat nie ELLA ideeeite tetra C Ti b) Tf he watches hwo filvs per month, how long until Hie other model. is worth ib? ia films pet month, we have m= 2. So now, 'pet film’ is C=3.5+5(m-4), so C=5m-15.. ‘Subscription’ is C=5.542m. See overpage for answerALGEBRAICALLY [Je can solve this “system to find Hie. poink: Hoe. “por Film’ model becomes more. txpeasive. C=5m-1.5 | GRAPH [2G] continued (/s) | 750 “subscription stoits Of as more expensive, Hach after 3.5 (4) motths, ib’s caeaper: | 5at-|5=5.5+3M 3 9M= C=5.5+3m, 1} | rT 1423.5. i.e: after been, E { “Ethie ig common, depending on Hue cluabion, lo ound up fr We (ital answer. Here, you ory pay once per mosh, 60 we Say ‘sub.’ iy worth ik afker 4: months. P Linear todels. are. common, ond. ta vost stigatforward. Many different: questions. could be asked about tom troughs. €.6.: Inkerprek intercepts, slopes, evaluating, eke. Pr¥or quadmtic. models, expect loks of. projectiles, Flying in.\-shaged pacabolas. Expect: to howe. bo work oukwhen. ik ‘wits the. ground.|sea’ by finding the roots /zeras, of finding tks vertex. (we eight), anvongst oH questions. €.G.2P Uganda had a pepulobion of lk:Bm on A374, and hos a grout wake of ~b.4% per year (a) Develop a model. for Uganda’s pop* ever bime.+ Colle. of years 6" (From tila) | pop: “p’(in willions). To. increase something oy 4A%, you.can multiply it by 1.044... uve get: P= 44.5 (1.0u9 b) Estimake He pop® of Uganda on 1/1/2028 + Lptug tn b=4: P=ud.6(1 04)" = 68. —> €2.t million people To €) The Ugardan. government as stated that dus to ds’ sual area, they don't Hairk Urey. could sustain a. populsikion more Haan 45 million people. te current pace, .whak montta vould. Haby pass this Figure? | 1 Soive Wi 5 (Lona)"=95 > Loutt=2.an83.. > b= log, (2. 0073.) — PE = 15.8530. C= 15 ye 10.24 n —> Which i November 2034 4) Tagan bod 126.5% poople in JOH, but is shvinting ak 2.4% ¢a.. aiuen should. Uganda's. pop* overtake Japan's ?ae oo aa ibaa wodel. ~ RERRESSIOND® You nay have Saal sere « model: ee roughly. FE Some neosuied data, “This model (eight) can be found pelea | tednnology..— i —e isa lmear model (a | straight line), and tis is a eet ak wil Le Learn in. mn in Tepic i] » near | "For Unese , you showd always be given He model in Hee. question. You will take those models, use Hem, conmient on them, or alter/extend them. Ch Ceiba on ar of alae pee pelican my include: You may Taal et aH Haak a. “differ APOLATION TF you have used data fron, Say: 2=2' bo x=10, you may have — a linear model Hhak Sits Wak date very. well. —You may. be fille be Holle ink | —regcession line. equakion 0 ond estimate a y-Volue for an | tn Ho daka. tf would be normal tp eskimake y. for, Say X= 8 (as 2<8<10). However, using Hae mcdel bo __ estimake for =\t is called extrapolahan. We caste kato for sure whak happens after 2 =10,/s0 Hris prockce is | seen as less reliable /useful. However, ib is, often