0 ratings0% found this document useful (0 votes) 53 views10 pagesUnit Three Partb-1
Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content,
claim it here.
Available Formats
Download as PDF or read online on Scribd
cO
Functions
By a functions we shall mean self-designed MATLAB script m-files which contain a few lines
of codes meant for executing a certain process. For instance, writing a function file for solving a
system of linear equations we have looked at briefly in Unit 2. Throughout our discussion in this
lesson, when we are to consider writing algorithms can be classified into two types: direct and
iterative methods. With the former, we obtain the solution in a finite number of steps, assuming.
no rounding errors, for example to solve a linear system with Gaussian elimination. Iterative
\n that converge to the
methods involve the process involves generating a sequence of approxim:
solution as the number of steps approaches infinity.
1, Writing function files
A basic function files structured in such a way that it has an output array, function file and input array
defined as
Oe
function [output}=function_name{input)
aeaaesese'reewewses
where input contains variable values defined by the user as to be used in the cade while function name
is the title of the file name for the script. However, itis not always the case that we specify the output.
For example we can have a structure either as
| function foutput}=function_nametinput)
Code
end
or
function function_nametinput)
code
(output)
end
‘Sometimes inputs are specified either inside the code or at the command window. As such, the structure
of the MATLAB function file changes and appears as,
59�function function_name
finput)
Main code
(output)
After the function declaration, say function [output]=function_name(input), in the m.file, it is
possible to write a description of the function. This is done with the comment sign “%” before
each fine. Then, from the command window, we can read this information about program's
description when we type “help”.
MATLAB will automatically generate a display when commands are executed. However, in
addition to this automatic display, MATLAB has several commands that can be used to generate
displays or outputs. Two commands that are frequently used to generate output are: disp and
printf.
Example
In order to compute the (N+1}-term Taylor series approximation to e* where e* = Sg, we write a
Matlab script file based on the following pseudo code;
Pseudo code
2xN>0
Inp
Output: (IV + 1)-term Taylor series approximation to e*
taylor=1; factorial=1; xpowk:
for ke1 toN, do
factorial = factorial * 2;
xpowk=xpowk*x;
taylor=taylor + (xpowk/factorial);
end
60�‘Thus, in Matlab, we implement the following code;
function [taylor] =Taylorestimate (x,N)
taylo!
factorial=1;
for k-1:N
factorial=factorial*k:
xpowk=xpowk*x;
taylor=taylor+ (x ;
end
disp ("The (N+1) approx to
evx is:')
end
With such a function file, to run, we type the main file line with inputs specified to get the results as
sylorestimate(2,10)
The (N+1)-term Taylor series approx to ex is:
taylor=
7.3890
Example
The following is a MATLAB fun
function
% FACTORIAL(N) returns the factorial of N
% Compute a factorial value.
rod(1:n);
Such that for n = 5, we get on the command window
>> f= factorial)
fe
| 120
61�2. Mathematical functions
‘A number of functions in MATLAB do not need to de defined or derived, however. For example, MATLAB
already offers many predefined mathematical functions “called built-ins” for technical computing which
contains a large set of mathematical functions. These functions can be accessed if we either type help
elfun or help specfun in the command window to call up full lists of elementary or special functions,
respectively.
Table 8 lists some commonly used functions, where variables x and y can be numbers, vectors, or
Toble 8: Elementary MATLAB built-in mathematical functions
matrices.
cosine
sine
tan(x) tangent
acos(x) arch cosine
asin(x) are sine
atan(x) are tangent
sqrt(x) square root
Jog(x) natural logarithm
Jogl0(x) standard logarithm
Example
To evaluate the expression y
following statements in MATLAB;
[oeanss
>>x=2;
>>ye8
>> y= expl-a)*sin(x)+10*sartly)
vy
28,2904
Example
abs(x) absolute value
sign(x) signum function
max(x)_ maximum value
min(x) minimum value
ceil(x) round towards +00
floor(x) round towards —o0
round(x) round to nearest integer
rem(x) remainder after division
angle(x) phase angle
complex conjugate
4 sin(x) + 10/y, for a = 5,x = 2 andy = 8, we type the
To evaluate the expression V = Inx + e!sin("/,) —logiox.
>>xe7;
>> Velog(x)+exp(10)}*sin{pi/4)-log10(x)
ve
1.5576e+04
62�3. Plot functions
The very basic plot function imbedded in MATLAB displays a graph of one’s interest in 2-
dimensional. For example, the function plot can be used to produce a graph from two vectors x
and y. Recall that a vector is an array of elements. This means by usage of vectors, we have two.
related arrays of elements whose plot can produce a graph.
During plotting, MATLAB is designed in such a way to plot one vector vs. another. The first one
is treated as the abscissa (or x) vector and the second as the ordinate (or y) vector. These vectors
have to be of the same length.
Besides, MATLAB can as well plot a vector vs. its own index. The index is therefore treated as
the abscissa vector. Given a vector “time” and a vector “dist” we could say:
>> plot (time, dist) % plotting versus time
>> plot (dist) % plotting versus index.
For instance, the follo¥rng-evse————
>> plot(xy)
produces a sine function graph whose x values range between —4 and 4, while y values range
between —1 and 1
Other than going just by mere plotting function, we also have MATLAB commands to annotate
the basic plot, by either adding axis labels, titles, and legends. These are defined by
>> xlabel (X-axis label’) % puts a label on x-axis, ]
>> ylabel (Y-axis uts 2 label on y-axis |
ylabel ("Y-axis label’) % puts a label on y: a
>> title (Title of my plot') % puts a title on the plot
>> legend|'Key features of my plot") % highlights key features of the plot�For example, try running the following statements on the MATLAB command window and
observe the differences in the outputs
[> x=-pi0 Apis y=sin(y)s
>> plot(xy)
>> plot(x,y,'s-')
>> xlabel('x'); ylabel(’
As another example, with a plot function file called aliasing, we can get
Function aliasing
xe =2:0.01:2;
E_xesin(-2*x) 7
guxesin (64x);
_xesin(-10°x) +
plot (x, f_x)7
hold 0
plot (x/¢_x);
hold off)
end
We can also add colors to the plotted lines for easy of distinguishing one line from the other in a
multiple plot. For example�>> x = O:pi/100:2* pi;
>> yl =24c0s(x);
>> y2-= cos(x);
y3 = 0.5%c08(x);
>> plot(x,yl.-1x,y2.X,93,"
>> xlabel(0 \leq x \leq 2\pi’)
>> ylabel(Cosine functions’)
>> legend('2*cos(x),'cos(x);'0.5*cos(x)’)
>> title("Typical example of multiple plots’)
>> axis({0 2*pi -3 3])
‘The color of a single curve is, by default, blue, but other colors are possible. In a plot function, the
desired color is indicated by a third argument. For example, red is selected by plot(xy,’r’). Note
the single quotes, ° ’, around r. By default, MATLAB uses line style and color to distinguish the
data sets plotted in the graph. However, we can change the appearance of these graphic
components or add annotations to the graph to help explain our data for presentation. Some of the
annotations are as presented in Table 9.
Table 9: Attributes for plot
Symbol [Color [Symbol [Line style [Symbol _| Marker
k Black = [Solid + __| Plus sign
r Red == [Dashed 0 _| Circle
a Blue z | Dotted * | Asterisk
Green =. _|Dash-dot ._| Point
c Cyan none __| No line x__| Cross
m. Magenta s__| Square
Yellow d___| Diamond
For example, it is possible to specify line styles, colors, and markers (e.g., circles, plus signs,...)
using the plot command:
where style_color_marker is a triplet of values from Table 9. For example by specifying asterisk
and circle style markers to our “aliasing” funetion, the plot looks change to
65�‘on aliasing
01:2;
n(-2*x) 5
IDxesin (67x) 5
27g_xesin(~
plot (x, £_x,
hold on
plot (x,¢_x,'0");
hold ©
end
Three-dimensional graphics can be produced using the imbedded functions surf, plot3 or mesh.
For example, upon writing and executing the following meshgrid plot function in the command
window
>> [X,Y] = meshgrid{-10:0.25:10,-10:0.25:10};
>> f= sine(sqrt((X/pi).*2+(¥/pi).*2));
>> mesh(XV.f);
>> axis([-10 10-10 10-03 1))
>> xlabel'{\bfx))
>> ylabel('\bfY')
>> zlabel('{\bfsinc} ({\bfR))')
>> hidden off
we get an output
As another example, with mesh plot function we can get
66�>> A = zer0s(32);
>> A(14:16,14:16) = ones(3);
>> Feabs(fft2(A)): °
>> mesh(F)
>> rotate3d on
Comparably, with surf plot function we can get
35 A= zeros(32);
>> A(14:16,14:16) = ones(3);
>> Feabs(fft2(A));
>> surfllF) q
>> rotate3d on .
Activity 3 b
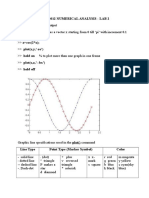
a) Plot the graph of the funetion f(x) = cosx + sin mx for x € [—27, 2] with 0.1 sub-
interval.
b) Write a function that shows an approximation for a factorial can be found using
Stirling’s formula:
w= Rn)
67�¢) Write a MATLAB function which should be able to find the volume and surface area
ofa cylinder when it’s closed at both ends.
4)" Write a script file that calls a function to prompt the user and read in values for the
hypotenuse and the angle (in radians), and then calls a function to calculate and return
the lengths of sides a and b, and a function to print out all values in a nice sentence
format.
¢) Write a for loop function to estimate V2 when t = [1,---,7] with reference to the
recurrence equation
for t = 1,23, yo
Re
Summary/Let Us Sum Up
‘To sum up, this unit was meant to introduce the student to the notion of counting, which is a key
principle and very fundamental to most real life application problems. With principles of counting,
techniques, the SUM RULE is noted to be useful for counting events that are made of collection
of independent events. On the other hand, the COMBINATORIAL RULE gives us a chance to
look at problems of making choices in life, which if we want to obtain such related unique choices,
68