Control Chart Selection
Variables / Measurements
❖ I-MR or X-MR chart (Individual, Moving Range)
❖ X bar - R chart (Average – Range)
❖ X bar - s chart (Average – Standard deviation)
Attributes / Counts
❖ np Chart (Number of defectives)
❖ p Chart (Proportion defectives)
❖ c Chart (Number of defects)
❖ u Chart (Number of defects per unit)
� Data Type
Attribute - Counts Variable - Measurements
# Pieces # Occurrences
# Defectives # Defects
Constant Variable Constant Variable n>9 n =2 to 9 n=1
np chart p chart c chart u chart Xbar - s Xbar - R I-MR/X-MR
n is subgroup size
� Control Chart Selection
Other Special Purpose Control Charts
❖ Short-run SPC
❖ Pre-Control Charts *
❖ Time Weighted Control Charts:
❖ Moving Average
❖ EWMA (Exponentially Weighted Moving
Average) *
❖ CUSUM (Cumulative Sum)*
� Time Weighted Control Charts
❖ Use the Moving Average Control Chart when
you want to quickly detect a change or shift in
the process.
❖ These charts are more sensitive to shifts in the
process than the traditional average and range
control chart.
❖ EWMA and CUSUM are more sensitive than
the Moving Average Chart
� Moving Average Control Charts
❖ Let’s use Minitab to plot the chart with Control
Limits.
❖ Manual calculation becomes complicated.
https://support.minitab.com/en-us/minitab/18/help-and-how-to/quality-and-
process-improvement/control-charts/how-to/time-weighted-charts/moving-
average-chart/methods-and-formulas/methods-and-formulas/
� Pre-Control Charts
❖ Use specification limits instead of
statistically-derived control limits to
determine process capability over time.
❖ Used during the initial setup process.
❖ Easier to setup, implement and interpret
�Pre-Control Charts
• Pre-Control Limits (LPCL and UPCL) are
50% of the tolerance.
• To establish process control, 5 items
should fall in the Pre-Control Limits.
• After that 2 successive units are
periodically samples.
• Continue if both fall in green or
one in green and one in Yellow.
• Stop and adjust process if both fall
in Yellow, or one fall in the red
zone.
� Short-run SPC
❖ A typical Control Chart needs 20-25
samples with 4 to 5 items as the
subgroup size.
❖ You need roughly 100 measurements to
define control limits.
❖ What if there are a very few pieces
manufactured?
❖ Use Short-run Chart
� Short-run SPC
❖ Short-run SPC focuses on the process
rather than the product.
❖ Example: Different diameter items
produced
❖ E.g Eight items with 300, 400 and 500 mm
each
❖ Options:
❖ 100% inspection – Expensive
❖ First-off inspection – What about process
variation?
❖ Last-off inspection – Too little too late
❖ Separate control chart – limited data
� Short-run SPC
302.634 Run A 504.188 Run B 400.548 Run C
300.558 Run A 506.879 Run B 403.193 Run C
301.604 Run A 506.189 Run B 392.790 Run C
298.130 Run A 517.210 Run B 399.538 Run C
298.824 Run A 479.511 Run B 392.192 Run C
301.384 Run A 495.170 Run B 403.812 Run C
302.373 Run A 506.851 Run B 393.457 Run C
298.685 Run A 489.671 Run B 401.051 Run C
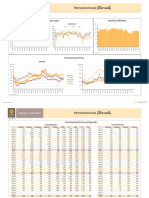
� Short-run – Difference Chart
Stamp Data
302.634
Run
Run A
Nominal
300
Difference
2.6338 Assumption: Each run has similar variance
300.558 Run A 300 0.5579
301.604 Run A 300 1.6043
298.130 Run A 300 -1.8704
298.824 Run A 300 -1.1757 I-MR Chart of C4
301.384 Run A 300 1.3837 20 UCL=21.16
302.373 Run A 300 2.3729
298.685 Run A 300 -1.3154 10
Individual Value
504.188 Run B 500 4.1884 0
_
X=-0.15
506.879 Run B 500 6.8792
-10
506.189 Run B 500 6.1887
517.210 Run B 500 17.2103 -20 LCL=-21.45
479.511 Run B 500 -20.4891 1 3 5 7 9 11 13 15 17 19 21 23
495.170 Run B 500 -4.8304 Observation
506.851 Run B 500 6.8514
40
489.671 Run B 500 -10.3293 1
400.548 Run C 400 0.5483 30
Moving Range
403.193 Run C 400 3.1932 UCL=26.17
20
392.790 Run C 400 -7.2102
399.538 Run C 400 -0.4623 10 __
MR=8.01
392.192 Run C 400 -7.8076
403.812 Run C 400 3.8119 0 LCL=0
1 3 5 7 9 11 13 15 17 19 21 23
393.457 Run C 400 -6.5428
Observation
401.051 Run C 400 1.0513
� Z-MR Chart
Stamp Data Run Nominal Difference
302.634 Run A 300 2.6338
300.558 Run A 300 0.5579
301.604 Run A 300 1.6043
298.130 Run A 300 -1.8704
298.824 Run A 300 -1.1757
301.384 Run A 300 1.3837
302.373 Run A 300 2.3729
298.685 Run A 300 -1.3154
504.188 Run B 500 4.1884
506.879 Run B 500 6.8792
506.189 Run B 500 6.1887
517.210 Run B 500 17.2103
479.511 Run B 500 -20.4891
495.170 Run B 500 -4.8304
506.851 Run B 500 6.8514
489.671 Run B 500 -10.3293
400.548 Run C 400 0.5483
403.193 Run C 400 3.1932
392.790 Run C 400 -7.2102
399.538 Run C 400 -0.4623
392.192 Run C 400 -7.8076
403.812 Run C 400 3.8119
393.457 Run C 400 -6.5428
401.051 Run C 400 1.0513