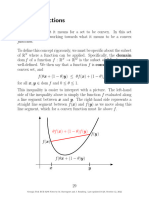
Some Properties of Convex Functions
The following properties are true for convex functions.
If f : Rn ! R is a convex function, then it is continuous over the interior of
dom(f ). Moreover, f is Lipschitz over every compact subset of the interior
of dom(f ).
If f and g are strictly convex functions, then f + g is strictly convex as well.
If f is a strongly convex function and g is a convex function, then f + g is
strongly convex as well.
47
� Level-set Characterization
Definition 15. For any ↵ 2 R, the level set of function f : Rn ! R̄ at level
↵ is defined as
lev↵ (f ) := {x 2 dom(f )|f (x) ↵}.
Proposition 15. If a function f is a convex function, then every level set
of f is a convex set.
In other words, if we can find some ↵ for which lev↵ (f ) is not a convex set, the
function f is not a convex function.
Converse is not true. A function is called quasi-convex if its domain and all level
sets are convex sets.
HW: Give an example of a function which is quasi-convex but not convex.
48
� Restriction of a Convex Function on a Line
Proposition 16. If a function f is convex if and only if for any x, h 2 Rn ,
the function (t) = f (x + th) is a convex function on R.
If we know how to check convexity of functions defined on R, then we can check
convexity of functions defined on Rn .
49
� First Order Condition
Proposition 17. If a function f is di↵erentiable, then it is convex if and
only if dom(f ) is a convex set and for any x, y 2 dom(f ), we have
f (y) f (x) + rf (x)> (y x).
A global lower bound on the function can be obtained at any point based on local
information (f (x), rf (x)).
50
� Second Order Condition
Proposition 18. If a function f is twice di↵erentiable, then it is convex if
and only if dom(f ) is a convex set and r2 f (y) ⌫ 0 for every y 2 dom(f ).
The function f is strongly convex if and only if r2 f (y) ⌫ mI for some
m > 0 for every y 2 dom(f ). Here I is the identity matrix of appropriate
dimension.
If r2 f (y) 0 for every y 2 dom(f ), then the function is strictly convex.
The converse is not true.
f is concave if and only if r2 f (y) 0 for every y 2 dom(f ).
Example: f (x) = x2 , log(x), ||Ax b||2 , and so on.
51
� Examples of Convex Functions
x> x
f1 (x, y) = y if y > 0 and +1 if y 0 (square to linear function).
Pn xi
f2 (x) = log( i=1 e ) (log-sum-exp function).
f3 (X) = log det(X) where X 2 S++
n (log-determinant function).
52
�Examples of Convex Functions
53
� Convexity Preserving Operations
Proposition 19 (Conic Combination). Let {fi (x)}i2I be a P
collection of con-
vex functions and let ↵i 0 for all i 2 I. Then, g(x) := i2I ↵i fi (x) is a
convex function.
Proposition 20 (Affine Composition). If f : Rm ! R is a convex function,
then g(x) := f (Ax + b) is also a convex function where A 2 Rm⇥n , b 2 Rm .
Pn >
Example: g(x) = ||Ax + b||2 , h(x) = i=1 log(ai x + b).
54
� Convexity Preserving Operations
Proposition 21 (Pointwise Maximum). Let {fi (x)}i2I is a collection of con-
vex functions, then g(x) := maxi2I fi (x) is a convex function.
The set I need not be a finite set.
Example: Largest singular value of a matrix X
f (X) = max (X) = max ||Xv||2 .
v:||v||2 =1
Proposition 22 (Pointwise Supremum). Let f (x, !) is convex in x for any
! 2 ⌦, then g(x) := sup!2⌦ f (x, !) is convex in x.
55
� Convexity Preserving Operations
Proposition 23 (Partial Minimization). If f (x, y) is convex in (x, y), and
Y is a convex set, then g(x) := inf y2Y f (x, y) is a convex function.
Example: Schur Complement Lemma
56
� Convexity Preserving Operations
Proposition 24 (Scalar Composition). Let f (x) := h(g(x)) where g : R ! R
and h : R ! R. Then, f is convex if
g is convex and h is convex non-decreasing
g is concave and h is convex non-increasing.
f is concave if
g is convex and h is concave non-increasing
g is concave and h is concave non-decreasing.
The conditions do not necessarily hold in the reverse direction.
57
� Convexity Preserving Operations
Proposition 25 (Vector Composition). Let {gi }i2{1,2,...k} are convex func-
tions on Rn , and h : Rk ! R is convex and non-decreasing in each argument,
then the function f (x) = h(g(x)) is convex.
Other scalar composition rules can also be directly extended to the vector case.
Examples:
If g is convex, then eg(x) is also convex.
1
If g is concave and positive, then g(x) is convex.
P
If gi are convex, then log( ki=1 egi (x) ) is convex.
58
� Recall: Optimization Problem
An optimization problem can be stated (in abstract form) as
min f (x), (2)
x2X
where
x decision variable, often a vector in Rn
X set of feasible solutions, often a subset of Rn
f : Rn ! R cost function
Goal:
Find x⇤ 2 X that minimizes the cost function, i.e., f (x⇤ ) f (x) for every
x 2 X.
Optimal value: f ⇤ := inf x2X f (x)
Optimal solution: x⇤ 2 X if f (x⇤ ) = f ⇤ .
Often, we write optimization problems in standard form as:
min f (x)
x2Rn
subject to gi (x) 0, i 2 {1, 2, . . . , m}
hj (x) = 0, j 2 {1, 2, . . . , p}.
59
� Recall
The problem is infeasible when X is an empty set. In this case, f ⇤ := +1.
The problem is unbounded when f ⇤ = 1.
Definition 16. Recall that
a feasible solution x⇤ 2 X is a global optimum if f (x⇤ ) f (x) for all
x 2 X. In this case, f ⇤ = f (x⇤ ),
the set of global optima: argminx2X f (x) := {z 2 X|f (z) = f ⇤ },
a feasible solution x⇤ 2 X is a local optimum if f (x⇤ ) f (x) for all
x 2 B(x⇤ , r) for some r > 0.
Theorem: Weierstrass Theorem
If the cost function f is continuous and the feasible region X is compact
(closed and bounded), then (at least one global) optimal solution x⇤ exists.
60
� Feasibility Problem
Goal: Find x 2 Rn which satisfies a collection of inequality and equality con-
straints.
min 0
x2Rn
subject to gi (x) 0, i 2 {1, 2, . . . , m}
hj (x) = 0, j 2 {1, 2, . . . , p}.
f ⇤ = 0 if a feasible solution exists. Otherwise, f ⇤ = +1.
61
� Convex Optimization Problems
An optimization problem in abstract form
min f (x), (3)
x2X
is convex when the feasibility set X is a convex set and the cost function f (x)
is a convex function.
An optimization problem in standard form
min f (x)
x2Rn
subject to gi (x) 0, i 2 {1, 2, . . . , m}
hj (x) = 0, j 2 {1, 2, . . . , p},
is convex when
f and gi are convex functions.
hj are affine functions.
62
�Simple Examples of Convex Functions
63
� 1. Local Optimum is Global
Theorem: Local and Global Optima
Consider the optimization problem minx2X f0 (x). If f0 is a convex function
and X is a convex set, then any locally optimal solution is also globally
optimal. Moreover, the set of optimal solutions Xopt := argminx2X f0 (x)
is a convex set.
64
� 2. Uniqueness under Strict Convexity
Theorem: Uniqueness under Strict Convexity
Consider the optimization problem minx2X f0 (x). If f0 is a strictly convex
function and X is a convex set, and x? is an optimal solution to the problem,
then, x? is the unique optimal solution, i.e., Xopt := {x? }.
65
� 3. Necessary and Sufficient Optimality Condition
Theorem: Necessary and Sufficient Optimality Condition
Consider the optimization problem minx2X f0 (x) where f0 is a convex and
di↵erentiable function, and X is a convex set. Then,
x? is optimal () rf0 (x? )> (y x? ) 0, 8y 2 X.
66
� Equivalent Optimization Problems
Consider the following two optimization problems:
min f (x). (4)
x2X
min g(y). (5)
y2Y
The above problems are equivalent if
Given an optimal solution x⇤ of (4), we can find an optimal solution y ⇤ of
(5), and
given an optimal solution y ⇤ of (5), we can find an optimal solution x⇤ of
(4).
67
�Equivalence: Maximization
68
�Equivalence: Epigraph Form
69
�Equivalence: Slack Variables
70
�Equivalence: From Equality to Inequality Constraints
71
�Equivalence: From Constrained to Unconstrained
72
�Equivalence: Scalar Multipliers and Constant Terms
73
�Equivalence: Monotone Transformations
74
�Inner Approximation
75
�Relaxation and Soft Constraints
76