0% found this document useful (0 votes)
85 views37 pagesSlide 6
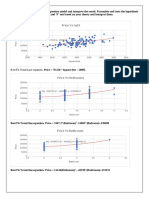
This document covers Chapter 6 of a course on Web Data Analysis, focusing on supervised learning and regression analysis. It includes topics such as linear regression, multiple linear regression, multi-collinearity, dummy variables, and logistic regression, along with methods for evaluating model performance. The chapter also discusses the implementation of logistic regression using scikit-learn.
Uploaded by
minhminh87882Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
85 views37 pagesSlide 6
This document covers Chapter 6 of a course on Web Data Analysis, focusing on supervised learning and regression analysis. It includes topics such as linear regression, multiple linear regression, multi-collinearity, dummy variables, and logistic regression, along with methods for evaluating model performance. The chapter also discusses the implementation of logistic regression using scikit-learn.
Uploaded by
minhminh87882Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 37