0% found this document useful (0 votes)
65 views31 pages3 Source Coding
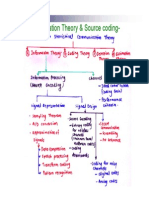
The document covers source coding in digital communication, detailing its applications and the principles of Shannon's Source Coding Theorem, which establishes the minimum bits required for encoding information based on entropy. It discusses various types of information sources and code types, including blocking, non-blocking, uniquely decodable, and instantaneous codes. Additionally, it explains fixed and variable length codes, their efficiencies, and the Kraft-McMillan inequality for prefix codes.
Uploaded by
adamsadsm0Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
65 views31 pages3 Source Coding
The document covers source coding in digital communication, detailing its applications and the principles of Shannon's Source Coding Theorem, which establishes the minimum bits required for encoding information based on entropy. It discusses various types of information sources and code types, including blocking, non-blocking, uniquely decodable, and instantaneous codes. Additionally, it explains fixed and variable length codes, their efficiencies, and the Kraft-McMillan inequality for prefix codes.
Uploaded by
adamsadsm0Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 31