100% found this document useful (2 votes)
212 views7 pagesCircle Theorems CSEC Notes With Diagrams
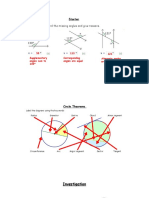
The document outlines key circle theorems relevant for CSEC Math, including the properties of angles in semicircles, cyclic quadrilaterals, and relationships between tangents and chords. Each theorem is accompanied by explanations, examples, and tips for application in exams. It emphasizes the importance of understanding these theorems for solving geometry problems effectively.
Uploaded by
kaikaiharris2008Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
100% found this document useful (2 votes)
212 views7 pagesCircle Theorems CSEC Notes With Diagrams
The document outlines key circle theorems relevant for CSEC Math, including the properties of angles in semicircles, cyclic quadrilaterals, and relationships between tangents and chords. Each theorem is accompanied by explanations, examples, and tips for application in exams. It emphasizes the importance of understanding these theorems for solving geometry problems effectively.
Uploaded by
kaikaiharris2008Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
/ 7