0% found this document useful (0 votes)
39 views17 pagesData Compression Unit-5
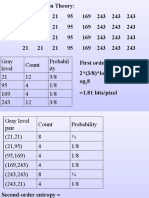
The document discusses entropy encoding, a lossless data compression method used in multimedia standards like JPEG and MPEG, which includes techniques such as Run Length Encoding (RLE) and Huffman coding. RLE compresses data by replacing sequences of identical symbols with a single symbol and a count, while Huffman coding assigns variable-length codes based on symbol probabilities to optimize compression. Additionally, Arithmetic Coding is introduced as a method that encodes entire messages into a single number based on symbol probabilities, allowing for efficient data representation.
Uploaded by
devil742638Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
39 views17 pagesData Compression Unit-5
The document discusses entropy encoding, a lossless data compression method used in multimedia standards like JPEG and MPEG, which includes techniques such as Run Length Encoding (RLE) and Huffman coding. RLE compresses data by replacing sequences of identical symbols with a single symbol and a count, while Huffman coding assigns variable-length codes based on symbol probabilities to optimize compression. Additionally, Arithmetic Coding is introduced as a method that encodes entire messages into a single number based on symbol probabilities, allowing for efficient data representation.
Uploaded by
devil742638Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 17