0% found this document useful (0 votes)
20 views42 pages01 Linear Regression
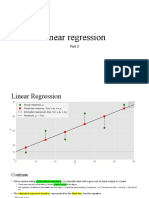
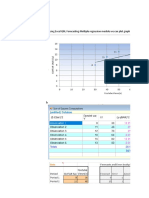
The document discusses linear regression, focusing on its application to advertising data to analyze the relationship between advertising budgets and product sales. It covers both simple and multiple linear regression, model selection, and the interpretation of coefficients, as well as statistical properties such as goodness-of-fit and hypothesis testing. The document emphasizes the importance of understanding linear relationships and the potential need for non-linear modeling in regression analysis.
Uploaded by
gedankenmankenCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
20 views42 pages01 Linear Regression
The document discusses linear regression, focusing on its application to advertising data to analyze the relationship between advertising budgets and product sales. It covers both simple and multiple linear regression, model selection, and the interpretation of coefficients, as well as statistical properties such as goodness-of-fit and hypothesis testing. The document emphasizes the importance of understanding linear relationships and the potential need for non-linear modeling in regression analysis.
Uploaded by
gedankenmankenCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 42