0% found this document useful (0 votes)
31 views43 pagesWeek 4 Multivariable Differentiation
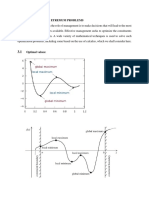
The document discusses implicit differentiation and directional derivatives, providing definitions and examples for both concepts. It explains how to compute directional derivatives using unit vectors and introduces the gradient as a vector-valued function. Additionally, it covers local extrema of functions of several variables, including critical points and the use of the discriminant to classify these points.
Uploaded by
chanjanCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
31 views43 pagesWeek 4 Multivariable Differentiation
The document discusses implicit differentiation and directional derivatives, providing definitions and examples for both concepts. It explains how to compute directional derivatives using unit vectors and introduces the gradient as a vector-valued function. Additionally, it covers local extrema of functions of several variables, including critical points and the use of the discriminant to classify these points.
Uploaded by
chanjanCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 43