0% found this document useful (0 votes)
28 views5 pagesCS Lab 2
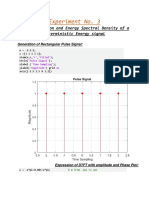
The document outlines an experiment in a B.Sc. Electrical Engineering course focused on implementing Energy Spectrum Density (ESD), Power Spectrum Density (PSD), and autocorrelation using MATLAB. It details the objectives, key concepts, procedure, MATLAB code, and expected plots for analyzing signal characteristics. The conclusion emphasizes the importance of ESD, PSD, and autocorrelation in understanding signal behavior and periodicity.
Uploaded by
M AqibCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
28 views5 pagesCS Lab 2
The document outlines an experiment in a B.Sc. Electrical Engineering course focused on implementing Energy Spectrum Density (ESD), Power Spectrum Density (PSD), and autocorrelation using MATLAB. It details the objectives, key concepts, procedure, MATLAB code, and expected plots for analyzing signal characteristics. The conclusion emphasizes the importance of ESD, PSD, and autocorrelation in understanding signal behavior and periodicity.
Uploaded by
M AqibCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
/ 5