2018/04/05

Introduction to milling II: Modelling

Population Balance Modelling (PBM) approach to milling i.e. kinetic approach

This method involves a more detailed modelling of the breakage of the material of
all the size fractions that the entire sample is comprised of.
After some grinding there will be
Feed changes in mass fractions
Product

Grinding mill

(i) The rate of how mass changes in

each fraction is modelled by the
selection function (S) parameter
(ii) Particle fragmentation
characteristics are modelled by
the breakage function (B)

Kinetics of Batch Milling

Grind for
time(t)

d (Wp1 )
= −S1Wp1 for particles in size-class 1
dt
S1: “selection function” ≡ first order rate constant for grinding
of particles in class 1. 0 2 4 6
Solution for p1(0) = p1 at t = 0: t(min.)
1
p1 (t ) = p1 (0)e − S1t or *
*
linear axis
p1 (t )
ln = − S 1t p (t ) *
p1 (0 ) 0.1 1
p (0) 1 *
• experimentally verified *
-s1
for many ores (some exceptions) *
• No good reason to justify this log axis
0.01
— loose probability argument.

1
 2018/04/05

First-order plot for traced coal ground in the presence of other

particles

Percentage of Irradiated Material in Fraction, w*(t)/w*(0)

Degree of grinding, revolutions

Conclusion: one class of particles does not interfere with the rate
of grinding of another class of particles (!)

How Selection function varies with size

10
Measured
Selection function (s-1)

Model

α
Austin et al have derived ad i
0.1 Si = Λ
model that fits this data d 
very well 1 +  i 
µ
0.01
0.1 1 10 100
Particle size (mm)

a is dependent on both material and grinding environment. α is generally believed to

be strongly linked to material properties. Λ and µ determines the point where the
selection function curve begins to decrease with increasing particle size.

2
 2018/04/05

Representation of the breakage function

1
b21

b31
b32
2
bn1
Breakage function matrix b for 4
bn2
size classes

3 0 0 0 0
b21 0 0 0
To the nth screen b31 b32 0 0
b41 b42 b43 0
n
In general bij =fraction broken into i when j is broken

Note some times it is more convenient to model bij as a cumulative function Bij and it is
relatively easy to reverse from one to the other

3
 2018/04/05

General model for batch operation

Size class 1 model
d (Wp1 )
= −S1Wp1
dt Before
Breakage
Similarly for class 2: moj m0j (t=0, mass
dp2 (t ) m0j in
= −S2 p2 (t ) + b21S1 p1 (t ) 2 1 class j)
dt
Substituting from equation for pL1(t): progeny lj Size
After
dp2 (t ) mij
+ S2 p2 (t ) = b21S1 p1 (0)e−S1t Breakage
dt mNj m unbroken
ij mj+1,j m
jj

which integrates to

b21S1 p1(0) −S1t −S2t −S t

p2 (t) = (e −e ) + p2 (0)e 2
S2 − S1

General model for batch operation

(cont.)
This may generalized as follows:
i
pi ( t ) = ∑d
j =1
ij p j (0)

where j −1

i<j − ∑ai k a jk i<j

0 k =i

dij =
e−S t
i −1
i
i=j
and aij = 1 i=j
∑ aik a jk (e
−Sk t
−e )
−Sit
1 i−1
∑ Sk bij akj
k= j
Si − S j k = j
i>j
i>j

4
 2018/04/05

Estimation of parameters in the batch milling model

• Do a series of batch tests on
several narrow size classes of
particles. Obtain the rate of
milling, Si for these classes.

Specific rate of breakage, min-1

• Use least-squares fitting to
estimate the parameters (a, α, μ)
in the equation: 1
S = a(xi / x0 )α [ ]
• Measure the full size distribution x
1+ ( i )Λ
obtained for short grinding times µ
(eg 30s; minimal secondary
breakage). Fit the batch grinding
model to this data in order to
estimate the parameters γ and φ Size xi, μm

in the breakage function.

γ β
• Typically Λ=3 and β=6 unless a x  x 
Bij ( xi , x j ) = φ  i −1  + (1 − φ ) i −1 
large amount of data is available.  x   x 
 j   j 

Class or Homework Exercise

• Assume you are interested in the behaviour of three
classes of particles during a batch test on the quartz
discussed in the previous slide:
– Class 1 : 600 to 850 micron; S1 = .7
– Class 2 : 300 to 600 micron; S2 = .45
– Class 3 : smaller than 300 micron; S3 = ?
• You are batch milling 1 kg of quartz particles which are all
between 850 and 600 micron at t = 0
• Calculate the mass of particles in classes 1, 2 and 3 after 1
minute. What additional data do you need? Assume a
value and proceed.

5
 2018/04/05

Grinding Simulation
• Rate of Breakage: Rate(di) = Sipi(di )W, kg/s

Si is a function of
• Ore type
• Equipment
• Operating S (min-1)
Conditions

Bij is a function of the

nature of the ore itself

d (µm)

The effect of ball diameter on

specific rates of breakage

Effect of Mill
Diameter
S (min-1)

d (µm)

6
 2018/04/05

The effect of ball diameter on

specific rates of breakage
S = a( x / x ) [ α 1
]
i 0
xi Λ
1+ ( )
µ

Effect of Mill
Diameter

S (min-1)

l (µm)

Effect of mass of coal (mill load) on milling rate

D=150mm, d=18mm,
J=0.5, N=78% crit
V V
U= particles
= particles
Where Voids εJVMill
V
ε = voidage, typically 0,4
J = load volume fraction
When U<<1 the grinding zones
between the balls are poorly
utilised.
When U > 1 the load is
expanded, ball-ball contact is
lost, mill goes “off the grind”

7
 2018/04/05

STEADY STATE SIMULATION OF A CONTINOUS MILL

for a specific size fraction i we consider the following:

1 Gain
Class i gains material as larger sizes breaks into
its faction and also when new feed enters with
class i material
2 Loss
F P Class i loses material due to breakage to lower
sizes and also when some of the i fraction
i leaves in the product

New
feed Product
The mass balance for class i at steady state can be
n
expressed as follows:
W i −1
Mill p i F = f i F + W ∑ bij S j w j − S i w iW
content j =1
i >1

where pi is the fraction of the product which is within size class i, F is the feed rate,fi is the
fraction of the feed that is within size class i, W is the weight of the material that is present
in the mill, while wi represents the fraction in the mill load of the size class i. Si is the
breakage rate and bij gives the fraction that breaks into size class i when breakage occurs in
size class j.

General Model for Continuous Operation

“Products of
breakage” bij SiWpi
F P
fi Pi
F Load T
fi W, pL diW pi
W, pL
(1-Si-di)Wpi
Dynamic mass balance on class i “idle”

IN + PRODUCED = OUT + BROKEN + ACCUM

i −1
d
Ff i + W ∑ bij s j w j = d iWwi + siWwi +
(Wwi )
j =1 dt
Divided by F; let θ = W/F; Matrix notation:
d B, S and D are NxN breakage,
pF + θBSpL = θ ( D + S ) pL + (θpL ) selection and discharge
dt
matrices

8
 2018/04/05

Selection Function Breakage Function

Matrix: Matrix:
S1 0 0 0 0 0 0 0
0 S2 0 0 b21 0 0 0
0 0 S3 0 b31 b32 0 0
0 0 0 S4 b41 b42 b43 0

Discharge Classification
Function Matrix:
d1 0 0 0 S4=?
0 d2 0 0 b4=?
0 0 d3 0
0 0 0 d4

d (θpL )
Steady – state operation: =0
dt
Solve for 1
p = (D+ S− B S) p −1

θ L F

*
Then pT = θD pL = D( D+ S − B S ) pF
−1

= T pF
T≡ Transformation Matrix

* obtained from TpTi = diWpLi; divide by T

9
 2018/04/05

Case (1)

Perfectly mixed mill, no classification at outlet, ie.

pT = p L
From our earlier equation we get
i−1
pFi = pTi + θ (Si pTi − ∑ S jbij pTj ) for i= 1…….N
j =1

Age can be 0
Start at i =1
to large values
pF1 = pT1 + ӨS1pT1
pF1 ……(1) Average age = θ
pT 1 =
1 + θS1

Perfectly mixed mill, no classification at outlet

for i=2 Age can be 0

to large values

pF2 = pT2 + Ө(S2pT2 – S1b21pT1)

Average age = θ

pF 2 + θS1b21 pT 1
∴ pT 2 =
1 + θS2

and further equations for pT3, pT4, etc can be obtained

in a similar manner.

10
 2018/04/05

Case 2: Plug Flow; no class at disch

F1 p F F1 pT
~ t
t=0 t=Ө

Each amount of feed spends a time Ө in the mill, so we

use
the batch milling equations with t = Ө.

Modelling Residence Time distribution (RTD)

The discharge pattern is

widely dispersed

Add salt in
time t

Hence both plug and mixed are not representative of real mill behavior, for short length mill
errors will be minimised

RTD is often approximated by using three mixed tanks in series (one large and 2 small tanks

1 2 3
70% 15% 15%

11
 2018/04/05

Discharge considerations

Classification at Discharge of the mill

Discharge aperture diam.

Discharg
e
Rate
Constant
, di
Particle Size
Discharge rate through the
discharge grate, TpTi = diWpLi

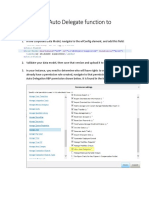
CUSTOMER INTERFACE FOR USING OUR MILLING MODELS

12