0% found this document useful (0 votes)
19 views42 pagesLecture 08
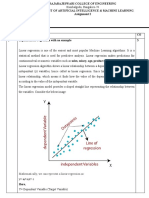
The document outlines a course on Machine Learning, covering key topics such as logistic regression, gradient descent, and various types of logistic regression models. It details the mechanics of gradient descent as an optimization algorithm, its applications in logistic regression, and the assumptions necessary for its implementation. Additionally, it discusses the advantages and properties of logistic regression, including its use in classification problems and the importance of sample size and independence of observations.
Uploaded by
shawon.iitju.48Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
19 views42 pagesLecture 08
The document outlines a course on Machine Learning, covering key topics such as logistic regression, gradient descent, and various types of logistic regression models. It details the mechanics of gradient descent as an optimization algorithm, its applications in logistic regression, and the assumptions necessary for its implementation. Additionally, it discusses the advantages and properties of logistic regression, including its use in classification problems and the importance of sample size and independence of observations.
Uploaded by
shawon.iitju.48Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 42