0% found this document useful (0 votes)
13 views5 pagesBisection Method Report
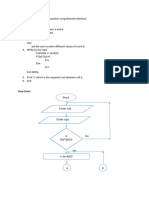
The document outlines a C++ program for finding roots of a non-linear equation using the Bisection method, which is effective for continuous functions that change sign over an interval. It includes the principle, theory, procedure, and algorithm for implementing the method, as well as a source code example. The program prompts the user for two initial guesses and iteratively narrows down the interval to locate the root with specified precision.
Uploaded by
Aswany SubramanianCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
13 views5 pagesBisection Method Report
The document outlines a C++ program for finding roots of a non-linear equation using the Bisection method, which is effective for continuous functions that change sign over an interval. It includes the principle, theory, procedure, and algorithm for implementing the method, as well as a source code example. The program prompts the user for two initial guesses and iteratively narrows down the interval to locate the root with specified precision.
Uploaded by
Aswany SubramanianCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
/ 5