0% found this document useful (0 votes)
22 views41 pagesUnit 7 Sorting
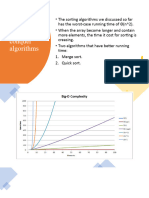
Chapter 8 discusses various sorting algorithms, categorizing them into internal and external sorting. It covers algorithms such as Bubble Sort, Selection Sort, Insertion Sort, Quick Sort, Merge Sort, Shell Sort, Exchange Sort, Radix Sort, and Heap Sort, detailing their methodologies, time complexities, and space complexities. The chapter emphasizes the importance of sorting in enhancing search efficiency and provides algorithms' pseudo codes and step-by-step processes.
Uploaded by
wivefa4443Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
22 views41 pagesUnit 7 Sorting
Chapter 8 discusses various sorting algorithms, categorizing them into internal and external sorting. It covers algorithms such as Bubble Sort, Selection Sort, Insertion Sort, Quick Sort, Merge Sort, Shell Sort, Exchange Sort, Radix Sort, and Heap Sort, detailing their methodologies, time complexities, and space complexities. The chapter emphasizes the importance of sorting in enhancing search efficiency and provides algorithms' pseudo codes and step-by-step processes.
Uploaded by
wivefa4443Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 41