0% found this document useful (0 votes)
78 views14 pagesCoordinate Geometry Ordinary Level
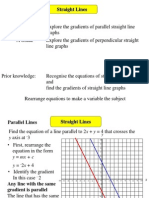
The document provides a comprehensive introduction to coordinate geometry, covering key concepts such as distance between points, midpoints, gradients of lines, and equations of straight lines. It includes definitions, formulas, and step-by-step examples to illustrate how to apply these concepts in solving mathematical problems. The content is aimed at helping learners understand and master the principles of coordinate geometry.
Uploaded by
serahzuze3Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
78 views14 pagesCoordinate Geometry Ordinary Level
The document provides a comprehensive introduction to coordinate geometry, covering key concepts such as distance between points, midpoints, gradients of lines, and equations of straight lines. It includes definitions, formulas, and step-by-step examples to illustrate how to apply these concepts in solving mathematical problems. The content is aimed at helping learners understand and master the principles of coordinate geometry.
Uploaded by
serahzuze3Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 14