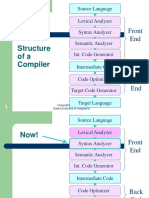
Lecture 6

Syntax Analysis

Awanish Pandey

Department of Computer Science and Engineering

Indian Institute of Technology
Roorkee

January 31, 2025

January 31, 2025 1 / 19

Take aways from the last class

Extended regular expressions

January 31, 2025 2 / 19

Take aways from the last class

Extended regular expressions

Lexical Analyzer generator

January 31, 2025 2 / 19

Take aways from the last class

Extended regular expressions

Lexical Analyzer generator
Lex file format and compilation steps

January 31, 2025 2 / 19

Take aways from the last class

Extended regular expressions

Lexical Analyzer generator
Lex file format and compilation steps
Working principle of the lex

January 31, 2025 2 / 19

Take aways from the last class

Extended regular expressions

Lexical Analyzer generator
Lex file format and compilation steps
Working principle of the lex
Correctness check of a string based on lex rules

January 31, 2025 2 / 19

Take aways from the last class

Extended regular expressions

Lexical Analyzer generator
Lex file format and compilation steps
Working principle of the lex
Correctness check of a string based on lex rules
Interface with other passes

January 31, 2025 2 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

January 31, 2025 3 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

Error reporting and recovery

January 31, 2025 3 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

Error reporting and recovery
Model using context-free grammars

January 31, 2025 3 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

Error reporting and recovery
Model using context-free grammars
Recognize using push-down automata/table-driven Parsers

January 31, 2025 3 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

Error reporting and recovery
Model using context-free grammars
Recognize using push-down automata/table-driven Parsers

To check whether variables are of types on which operations are allowed

January 31, 2025 3 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

Error reporting and recovery
Model using context-free grammars
Recognize using push-down automata/table-driven Parsers

To check whether variables are of types on which operations are allowed ✗

January 31, 2025 3 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

Error reporting and recovery
Model using context-free grammars
Recognize using push-down automata/table-driven Parsers

To check whether variables are of types on which operations are allowed ✗

To check whether a variable has been declared before use

January 31, 2025 3 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

Error reporting and recovery
Model using context-free grammars
Recognize using push-down automata/table-driven Parsers

To check whether variables are of types on which operations are allowed ✗

To check whether a variable has been declared before use ✗

January 31, 2025 3 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

Error reporting and recovery
Model using context-free grammars
Recognize using push-down automata/table-driven Parsers

To check whether variables are of types on which operations are allowed ✗

To check whether a variable has been declared before use ✗
To check whether a variable has been initialized

January 31, 2025 3 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

Error reporting and recovery
Model using context-free grammars
Recognize using push-down automata/table-driven Parsers

To check whether variables are of types on which operations are allowed ✗

To check whether a variable has been declared before use ✗
To check whether a variable has been initialized ✗

January 31, 2025 3 / 19

Overview of Syntax Analysis

Check syntax and construct abstract syntax tree

Error reporting and recovery
Model using context-free grammars
Recognize using push-down automata/table-driven Parsers

To check whether variables are of types on which operations are allowed ✗

To check whether a variable has been declared before use ✗
To check whether a variable has been initialized ✗
These issues will be handled in semantic analysis

January 31, 2025 3 / 19

Derivation

Does 9 − 5 + 2 belong to the following grammar?

list → list + digit
|list − digit
|digit
digit → 0|1|2 . . . |9

January 31, 2025 4 / 19

Derivation

Does 9 − 5 + 2 belong to the following grammar?

list → list + digit
|list − digit
|digit
digit → 0|1|2 . . . |9
String Derivation:

January 31, 2025 4 / 19

Derivation

Does 9 − 5 + 2 belong to the following grammar?

list → list + digit
|list − digit
|digit
digit → 0|1|2 . . . |9
String Derivation:
list → list + digit

January 31, 2025 4 / 19

Derivation

Does 9 − 5 + 2 belong to the following grammar?

list → list + digit
|list − digit
|digit
digit → 0|1|2 . . . |9
String Derivation:
list → list + digit
list → list − digit + digit

January 31, 2025 4 / 19

Derivation

Does 9 − 5 + 2 belong to the following grammar?

list → list + digit
|list − digit
|digit
digit → 0|1|2 . . . |9
String Derivation:
list → list + digit
list → list − digit + digit
list → digit − digit + digit

January 31, 2025 4 / 19

Derivation

Does 9 − 5 + 2 belong to the following grammar?

list → list + digit
|list − digit
|digit
digit → 0|1|2 . . . |9
String Derivation:
list → list + digit
list → list − digit + digit
list → digit − digit + digit
list → 9 − digit + digit

January 31, 2025 4 / 19

Derivation

Does 9 − 5 + 2 belong to the following grammar?

list → list + digit
|list − digit
|digit
digit → 0|1|2 . . . |9
String Derivation:
list → list + digit
list → list − digit + digit
list → digit − digit + digit
list → 9 − digit + digit
list → 9 − 5 + digit

January 31, 2025 4 / 19

Derivation

Does 9 − 5 + 2 belong to the following grammar?

list → list + digit
|list − digit
|digit
digit → 0|1|2 . . . |9
String Derivation:
list → list + digit
list → list − digit + digit
list → digit − digit + digit
list → 9 − digit + digit
list → 9 − 5 + digit
list → 9 − 5 + 2

January 31, 2025 4 / 19

Derivation

Does 9 − 5 + 2 belong to the following grammar?

list → list + digit
|list − digit
|digit
digit → 0|1|2 . . . |9
String Derivation:
list → list + digit
list → list − digit + digit
list → digit − digit + digit Which non-terminal should I choose?
list → 9 − digit + digit
list → 9 − 5 + digit
list → 9 − 5 + 2

January 31, 2025 4 / 19

Derivation

Does 9 − 5 + 2 belong to the following grammar?

list → list + digit
|list − digit
|digit
digit → 0|1|2 . . . |9
String Derivation:
list → list + digit
list → list − digit + digit
list → digit − digit + digit Which non-terminal should I choose?
list → 9 − digit + digit Which production rule should I select?
list → 9 − 5 + digit
list → 9 − 5 + 2

January 31, 2025 4 / 19

Derivation

If there is a production A → α then we say that A derives α and is denoted by A ⇒ α

January 31, 2025 5 / 19

Derivation

If there is a production A → α then we say that A derives α and is denoted by A ⇒ α

αAβ ⇒ αγβ if A → γ is a production

January 31, 2025 5 / 19

Derivation

If there is a production A → α then we say that A derives α and is denoted by A ⇒ α

αAβ ⇒ αγβ if A → γ is a production
If α1 ⇒ α2 ⇒ · · · ⇒ αn then α1 ⇒+ αn

January 31, 2025 5 / 19

Derivation

If there is a production A → α then we say that A derives α and is denoted by A ⇒ α

αAβ ⇒ αγβ if A → γ is a production
If α1 ⇒ α2 ⇒ · · · ⇒ αn then α1 ⇒+ αn
If S ⇒+ α where α is a string of terminals and non-terminals of G then we say that α is
a sentential form of G.

January 31, 2025 5 / 19

Derivation

If there is a production A → α then we say that A derives α and is denoted by A ⇒ α

αAβ ⇒ αγβ if A → γ is a production
If α1 ⇒ α2 ⇒ · · · ⇒ αn then α1 ⇒+ αn
If S ⇒+ α where α is a string of terminals and non-terminals of G then we say that α is
a sentential form of G.
If in a sentential form only the leftmost non terminal is replaced then it becomes leftmost
derivation

January 31, 2025 5 / 19

Derivation

If there is a production A → α then we say that A derives α and is denoted by A ⇒ α

αAβ ⇒ αγβ if A → γ is a production
If α1 ⇒ α2 ⇒ · · · ⇒ αn then α1 ⇒+ αn
If S ⇒+ α where α is a string of terminals and non-terminals of G then we say that α is
a sentential form of G.
If in a sentential form only the leftmost non terminal is replaced then it becomes leftmost
derivation
Every leftmost step can be written as wAγ ⇒lm∗ w δγ where w is a string of terminals
and A → δ is a production.

January 31, 2025 5 / 19

Derivation

If there is a production A → α then we say that A derives α and is denoted by A ⇒ α

αAβ ⇒ αγβ if A → γ is a production
If α1 ⇒ α2 ⇒ · · · ⇒ αn then α1 ⇒+ αn
If S ⇒+ α where α is a string of terminals and non-terminals of G then we say that α is
a sentential form of G.
If in a sentential form only the leftmost non terminal is replaced then it becomes leftmost
derivation
Every leftmost step can be written as wAγ ⇒lm∗ w δγ where w is a string of terminals
and A → δ is a production.
Similarly, right most derivation can be defined.

January 31, 2025 5 / 19

Derivation

If there is a production A → α then we say that A derives α and is denoted by A ⇒ α

αAβ ⇒ αγβ if A → γ is a production
If α1 ⇒ α2 ⇒ · · · ⇒ αn then α1 ⇒+ αn
If S ⇒+ α where α is a string of terminals and non-terminals of G then we say that α is
a sentential form of G.
If in a sentential form only the leftmost non terminal is replaced then it becomes leftmost
derivation
Every leftmost step can be written as wAγ ⇒lm∗ w δγ where w is a string of terminals
and A → δ is a production.
Similarly, right most derivation can be defined.
An ambiguous grammar is one that produces more than one leftmost/rightmost
derivation of a sentence

January 31, 2025 5 / 19

Parse Tree

It shows how the start symbol of a grammar derives a string in the language.

January 31, 2025 6 / 19

Parse Tree

It shows how the start symbol of a grammar derives a string in the language.
root is labeled by the start symbol

January 31, 2025 6 / 19

Parse Tree

It shows how the start symbol of a grammar derives a string in the language.
root is labeled by the start symbol
leaf nodes are labeled by tokens

January 31, 2025 6 / 19

Parse Tree

It shows how the start symbol of a grammar derives a string in the language.
root is labeled by the start symbol
leaf nodes are labeled by tokens
Each internal node is labeled by a non-terminal

January 31, 2025 6 / 19

Parse Tree

It shows how the start symbol of a grammar derives a string in the language.
root is labeled by the start symbol
leaf nodes are labeled by tokens
Each internal node is labeled by a non-terminal
If A is a non-terminal labeling an internal node and x1 , x2 , . . . xn are labels of the children
of that node, then A → x1 x2 . . . xn is a production

January 31, 2025 6 / 19

Ambiguity

January 31, 2025 7 / 19

Ambiguity
A Grammar can have more than one parse tree for a string

January 31, 2025 7 / 19

Ambiguity
A Grammar can have more than one parse tree for a string
Consider grammar

January 31, 2025 7 / 19

Ambiguity
A Grammar can have more than one parse tree for a string
Consider grammar
string → string + string
|string − string
|0|1|· · · |9

January 31, 2025 7 / 19

Ambiguity
A Grammar can have more than one parse tree for a string
Consider grammar
string → string + string
|string − string
|0|1|· · · |9
String 9 − 5 + 2 has two parse trees

January 31, 2025 7 / 19

Ambiguity
A Grammar can have more than one parse tree for a string
Consider grammar
string → string + string
|string − string
|0|1|· · · |9
String 9 − 5 + 2 has two parse trees

January 31, 2025 7 / 19

Ambiguity

Ambiguity is problematic because meaning of the programs can be incorrect

January 31, 2025 8 / 19

Ambiguity

Ambiguity is problematic because meaning of the programs can be incorrect

Ambiguity can be handled in several ways

January 31, 2025 8 / 19

Ambiguity

Ambiguity is problematic because meaning of the programs can be incorrect

Ambiguity can be handled in several ways
▶ Enforce associativity and precedence

January 31, 2025 8 / 19

Ambiguity

Ambiguity is problematic because meaning of the programs can be incorrect

Ambiguity can be handled in several ways
▶ Enforce associativity and precedence
▶ Rewrite the grammar (cleanest way)

January 31, 2025 8 / 19

Ambiguity

Ambiguity is problematic because meaning of the programs can be incorrect

Ambiguity can be handled in several ways
▶ Enforce associativity and precedence
▶ Rewrite the grammar (cleanest way)
There are no general techniques for handling ambiguity

January 31, 2025 8 / 19

Ambiguity

Ambiguity is problematic because meaning of the programs can be incorrect

Ambiguity can be handled in several ways
▶ Enforce associativity and precedence
▶ Rewrite the grammar (cleanest way)
There are no general techniques for handling ambiguity
It is impossible to convert automatically an ambiguous grammar to an unambiguous one.

January 31, 2025 8 / 19

Associativity and Precedence

If an operand has operators on both of the sides, the side on which operators takes this
operand is the associativity of that operator.

January 31, 2025 9 / 19

Associativity and Precedence

If an operand has operators on both of the sides, the side on which operators takes this
operand is the associativity of that operator.
In a + b + c b is taken by left +

January 31, 2025 9 / 19

Associativity and Precedence

If an operand has operators on both of the sides, the side on which operators takes this
operand is the associativity of that operator.
In a + b + c b is taken by left +
+, −, ∗, / are left associative

January 31, 2025 9 / 19

Associativity and Precedence

If an operand has operators on both of the sides, the side on which operators takes this
operand is the associativity of that operator.
In a + b + c b is taken by left +
+, −, ∗, / are left associative
ˆ= are right associative

January 31, 2025 9 / 19

Associativity and Precedence

If an operand has operators on both of the sides, the side on which operators takes this
operand is the associativity of that operator.
In a + b + c b is taken by left +
+, −, ∗, / are left associative
ˆ= are right associative
String a+5*2 has two possible interpretations because of two different parse trees
corresponding to (a + 5) ∗ 2 and a + (5 ∗ 2).

January 31, 2025 9 / 19

Associativity and Precedence

If an operand has operators on both of the sides, the side on which operators takes this
operand is the associativity of that operator.
In a + b + c b is taken by left +
+, −, ∗, / are left associative
ˆ= are right associative
String a+5*2 has two possible interpretations because of two different parse trees
corresponding to (a + 5) ∗ 2 and a + (5 ∗ 2).
Precedence determines the correct interpretation.

January 31, 2025 9 / 19

Ambiguity

Dangling else problem

January 31, 2025 10 / 19

Ambiguity

Dangling else problem

Stmt → if expr then stmt
|if expr then stmt else stmt

January 31, 2025 10 / 19

Ambiguity

Dangling else problem

Stmt → if expr then stmt
|if expr then stmt else stmt
if el then if e2 then S1 else S2 has two parse trees

January 31, 2025 10 / 19

Ambiguity

Dangling else problem

Stmt → if expr then stmt
|if expr then stmt else stmt
if el then if e2 then S1 else S2 has two parse trees
if(e1)
if(e2)
S1
else
S2

January 31, 2025 10 / 19

Ambiguity

Dangling else problem

Stmt → if expr then stmt
|if expr then stmt else stmt
if el then if e2 then S1 else S2 has two parse trees
if(e1) if(e1)
if(e2) if(e2)
S1 S1
else else
S2 S2

January 31, 2025 10 / 19

Resolving dangling else problem

Match each else with the closest previous then

January 31, 2025 11 / 19

Resolving dangling else problem

Match each else with the closest previous then

stmt → matched-stmt
| unmatched-stmt

January 31, 2025 11 / 19

Resolving dangling else problem

Match each else with the closest previous then

stmt → matched-stmt
| unmatched-stmt
matched-stmt → if expr then matched-stmt else matched-stmt
|others

January 31, 2025 11 / 19

Resolving dangling else problem

Match each else with the closest previous then

stmt → matched-stmt
| unmatched-stmt
matched-stmt → if expr then matched-stmt else matched-stmt
|others
unmatched-stmt → if expr then stmt
| if expr then matched-stmt else unmatched-stmt

January 31, 2025 11 / 19

Parsing

Process of determination whether a string can be generated by a grammar.

January 31, 2025 12 / 19

Parsing

Process of determination whether a string can be generated by a grammar.

Parsing falls in two categories:

January 31, 2025 12 / 19

Parsing

Process of determination whether a string can be generated by a grammar.

Parsing falls in two categories:
▶ Top-down parsing: Construction of the parse tree starts at the root (from the start symbol)
and proceeds towards leaves (token or terminals). Ex ANTLR

January 31, 2025 12 / 19

Parsing

Process of determination whether a string can be generated by a grammar.

Parsing falls in two categories:
▶ Top-down parsing: Construction of the parse tree starts at the root (from the start symbol)
and proceeds towards leaves (token or terminals). Ex ANTLR
▶ Bottom-up parsing: Construction of the parse tree starts from the leaf nodes (tokens or
terminals of the grammar) and proceeds towards root (start symbol). Ex YACC and BISON

January 31, 2025 12 / 19

Top Down Parsing

Construction of a parse tree is done by starting the root labeled by a start symbol

January 31, 2025 13 / 19

Top Down Parsing

Construction of a parse tree is done by starting the root labeled by a start symbol
repeat following two steps

January 31, 2025 13 / 19

Top Down Parsing

Construction of a parse tree is done by starting the root labeled by a start symbol
repeat following two steps
▶ at a node labeled with non terminal A select one of the productions of A and construct
children nodes (Which production?)

January 31, 2025 13 / 19

Top Down Parsing

Construction of a parse tree is done by starting the root labeled by a start symbol
repeat following two steps
▶ at a node labeled with non terminal A select one of the productions of A and construct
children nodes (Which production?)
▶ find the next node at which subtree is Constructed (Which node?)

January 31, 2025 13 / 19

Top Down Parsing

Construction of a parse tree is done by starting the root labeled by a start symbol
repeat following two steps
▶ at a node labeled with non terminal A select one of the productions of A and construct
children nodes (Which production?)
▶ find the next node at which subtree is Constructed (Which node?)

January 31, 2025 13 / 19

Recursive Descent parsing

Algorithm A()
1: Choose an A-production, A → X1 X2 · · · Xk
2: for i = 1 to k do
3: if Xi is a nonterminal then
4: call procedureXi ()
5: else if Xi equals the current input symbol α then
6: advance the input to the next symbol
7: else
8: error()
9: end if
10: end for

January 31, 2025 14 / 19

Recursive Descent parsing

Non-deterministic due to line 1 of the Algorithm 1

January 31, 2025 15 / 19

Recursive Descent parsing

Non-deterministic due to line 1 of the Algorithm 1

Require backtracking

January 31, 2025 15 / 19

Recursive Descent parsing

Non-deterministic due to line 1 of the Algorithm 1

Require backtracking
May require repeated scans over the input.

January 31, 2025 15 / 19

Recursive Descent parsing

Non-deterministic due to line 1 of the Algorithm 1

Require backtracking
May require repeated scans over the input.
Dynamic Programming or tabular method may be used.

January 31, 2025 15 / 19

Left Recursion

A top-down parser with production A → Aα may loop forever.

January 31, 2025 16 / 19

Left Recursion

A top-down parser with production A → Aα may loop forever.

From the grammar A → Aα|β left recursion may be eliminated by transforming the
grammar to

January 31, 2025 16 / 19

Left Recursion

A top-down parser with production A → Aα may loop forever.

From the grammar A → Aα|β left recursion may be eliminated by transforming the
grammar to
A → βR

January 31, 2025 16 / 19

Left Recursion

A top-down parser with production A → Aα may loop forever.

From the grammar A → Aα|β left recursion may be eliminated by transforming the
grammar to
A → βR
R → αR|ϵ

January 31, 2025 16 / 19

Left Recursion

A top-down parser with production A → Aα may loop forever.

From the grammar A → Aα|β left recursion may be eliminated by transforming the
grammar to
A → βR
R → αR|ϵ
In general A → Aα1 |Aα2 | · · · |Aαm |β1 |β2 | · · · |βn transforms to

January 31, 2025 16 / 19

Left Recursion

A top-down parser with production A → Aα may loop forever.

From the grammar A → Aα|β left recursion may be eliminated by transforming the
grammar to
A → βR
R → αR|ϵ
In general A → Aα1 |Aα2 | · · · |Aαm |β1 |β2 | · · · |βn transforms to
A → β1 A′ |β2 A′ | · · · |βn A′
A′ → α1 A′ |α2 A′ | · · · |αm A′ |ϵ

January 31, 2025 16 / 19

Example

Consider grammar for arithmetic expressions

E → E + T |T
T → T ∗ F |F
F → (E )|id

January 31, 2025 17 / 19

Example

Consider grammar for arithmetic expressions

E → E + T |T
T → T ∗ F |F
F → (E )|id
After removal of left recursion the grammar becomes

January 31, 2025 17 / 19

Example

Consider grammar for arithmetic expressions

E → E + T |T
T → T ∗ F |F
F → (E )|id
After removal of left recursion the grammar becomes
E → TE ′
E ′ → +TE ′ |ϵ
T → FT ′
T ′ → ∗FT ′ |ϵ
F → (E )|id

January 31, 2025 17 / 19

Left recursion hidden due to many productions
Left recursion may also be introduced by two or more grammar rules. For example:
S → Aa|b
A → Ac|Sd|ϵ

January 31, 2025 18 / 19

Left recursion hidden due to many productions
Left recursion may also be introduced by two or more grammar rules. For example:
S → Aa|b
A → Ac|Sd|ϵ
Hidden left recursion due to S → Aa → Sda

January 31, 2025 18 / 19

Left recursion hidden due to many productions
Left recursion may also be introduced by two or more grammar rules. For example:
S → Aa|b
A → Ac|Sd|ϵ
Hidden left recursion due to S → Aa → Sda
Remove left recursion systematically.

January 31, 2025 18 / 19

Left recursion hidden due to many productions
Left recursion may also be introduced by two or more grammar rules. For example:
S → Aa|b
A → Ac|Sd|ϵ
Hidden left recursion due to S → Aa → Sda
Remove left recursion systematically.
▶ Starting from the first rule and replacing all the occurrences of the first non terminal symbol.

January 31, 2025 18 / 19

Left recursion hidden due to many productions
Left recursion may also be introduced by two or more grammar rules. For example:
S → Aa|b
A → Ac|Sd|ϵ
Hidden left recursion due to S → Aa → Sda
Remove left recursion systematically.
▶ Starting from the first rule and replacing all the occurrences of the first non terminal symbol.
▶ Removing left recursion from the modified grammar.

January 31, 2025 18 / 19

Left recursion hidden due to many productions
Left recursion may also be introduced by two or more grammar rules. For example:
S → Aa|b
A → Ac|Sd|ϵ
Hidden left recursion due to S → Aa → Sda
Remove left recursion systematically.
▶ Starting from the first rule and replacing all the occurrences of the first non terminal symbol.
▶ Removing left recursion from the modified grammar.
After the first step (substitute S by its rhs in the rules) the grammar becomes

January 31, 2025 18 / 19

Left recursion hidden due to many productions
Left recursion may also be introduced by two or more grammar rules. For example:
S → Aa|b
A → Ac|Sd|ϵ
Hidden left recursion due to S → Aa → Sda
Remove left recursion systematically.
▶ Starting from the first rule and replacing all the occurrences of the first non terminal symbol.
▶ Removing left recursion from the modified grammar.
After the first step (substitute S by its rhs in the rules) the grammar becomes
S → Aa|b
A → Ac|Aad|bd|ϵ

January 31, 2025 18 / 19

Left recursion hidden due to many productions
Left recursion may also be introduced by two or more grammar rules. For example:
S → Aa|b
A → Ac|Sd|ϵ
Hidden left recursion due to S → Aa → Sda
Remove left recursion systematically.
▶ Starting from the first rule and replacing all the occurrences of the first non terminal symbol.
▶ Removing left recursion from the modified grammar.
After the first step (substitute S by its rhs in the rules) the grammar becomes
S → Aa|b
A → Ac|Aad|bd|ϵ
After the second step (removal of left recursion) the grammar becomes

January 31, 2025 18 / 19

Left recursion hidden due to many productions
Left recursion may also be introduced by two or more grammar rules. For example:
S → Aa|b
A → Ac|Sd|ϵ
Hidden left recursion due to S → Aa → Sda
Remove left recursion systematically.
▶ Starting from the first rule and replacing all the occurrences of the first non terminal symbol.
▶ Removing left recursion from the modified grammar.
After the first step (substitute S by its rhs in the rules) the grammar becomes
S → Aa|b
A → Ac|Aad|bd|ϵ
After the second step (removal of left recursion) the grammar becomes
S → Aa|b
A → bdA′ |A′
A′ → cA′ |adA′ |ϵ

January 31, 2025 18 / 19

Left Factoring

In top-down parsing when it is not clear which production to choose for expansion of a
symbol defer the decision till we have seen enough input.

January 31, 2025 19 / 19

Left Factoring

In top-down parsing when it is not clear which production to choose for expansion of a
symbol defer the decision till we have seen enough input.
A → αβ1 |αβ2 transforms to

January 31, 2025 19 / 19

Left Factoring

In top-down parsing when it is not clear which production to choose for expansion of a
symbol defer the decision till we have seen enough input.
A → αβ1 |αβ2 transforms to
A → αA′
A′ → β1 |β2

January 31, 2025 19 / 19