0% found this document useful (0 votes)
55 views10 pages2D Viewing Notes
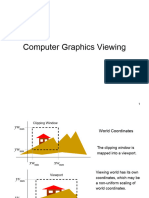
The document discusses computer graphics concepts such as windowing, viewport, and the transformation process between them. It explains clipping techniques for points, lines, polygons, and text, detailing algorithms like Cohen-Sutherland and Sutherland-Hodgman for efficient rendering. Additionally, it covers curve clipping and the importance of coordinate transformations in displaying objects on a screen.
Uploaded by
Alok ChoudharyCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
55 views10 pages2D Viewing Notes
The document discusses computer graphics concepts such as windowing, viewport, and the transformation process between them. It explains clipping techniques for points, lines, polygons, and text, detailing algorithms like Cohen-Sutherland and Sutherland-Hodgman for efficient rendering. Additionally, it covers curve clipping and the importance of coordinate transformations in displaying objects on a screen.
Uploaded by
Alok ChoudharyCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 10